Ios教程網 >> IOS編程開發 >> IOS開發基礎 >> CoreAnimation初探(一) —— 圖形學基礎

CoreAnimation初探(一) —— 圖形學基礎

編輯：IOS開發基礎

關於CoreAnimation

CoreAnimation是蘋果提供的一套基於繪圖的動畫框架，下圖是官方文檔中給出的體系結構。

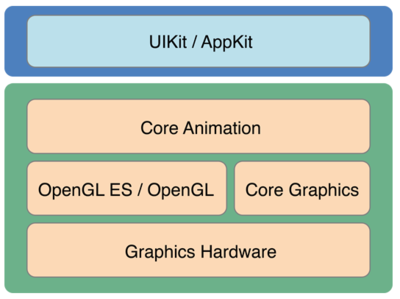
CoreAnimation所在位置

從圖中可以看出，最底層是圖形硬件(GPU)；上層是OpenGL和CoreGraphics，提供一些接口來訪問GPU；再上層的CoreAnimation在此基礎上封裝了一套動畫的API。最上面的UIKit屬於應用層，處理與用戶的交互。所以，學習CoreAnimation也會涉及一些圖形學的知識，了解這些有助於我們更順手的使用以及更高效的解決問題。本篇從以下幾點簡單整理了一些圖形學的知識，以對其中原理有個概念上的認識。

什麼是圖形學

圖形變換

曲線和曲面

1.什麼是圖形學

簡單的說，計算機圖形學是指用計算機產生對象圖形輸出的技術。更確切的說，是研究通過計算機將數據轉換為圖形，並在專門顯示設備上顯示的原理、方法和技術的學科。

舉一個簡單的例子，如果只提供給我們一個方法setPixel(x,y)用來點亮屏幕上坐標為(x,y)的像素點，如何在兩點(x1,y1)、(x2,y2)之間畫一條直線呢？（這是圖形學研究的一個最基本問題：圖形基元的顯示。圖形基元指一些基本的集合圖形，如線段、圓、多邊形等。）

我們最容易想到、也是最直接的方法便是計算出該直線在每個整數點對應的坐標值，四捨五入點亮與其最近的像素點（稱為數值微分分析，DDA），如下圖所示。

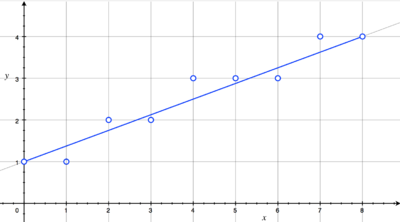
直線掃描轉換（斜率<1時）

但這種方法有很大的缺點：對於直線y=mx+b，我們在計算每個整數點坐標時，需要一次乘法和一次加法運算。而m、b都不一定是整數，所以更准確的說是浮點數乘法，這對於底層硬件實現是很傷的。

基於這種消除乘法和浮點數運算的思想便有了中心點畫線法。
首先對於消除乘法運算，不必每次算坐標時都乘以斜率m，而是采用增量計算的方法；
而對於消除浮點數，則可以使用只含整數參數的直線方程計算：ax+by+c=0（這裡a,b,c可以都為整數，因為我們的起點(x1,y1)和終點(x2,y2)是屏幕上的像素點一定都為整數，可以計算得出一個滿足條件的整數方程：a=y1-y2, b=x2-x1, c=x1y2-x2y1）。

為方便討論我們仍假設直線的斜率<1，在循環點亮路徑上的像素點時，x坐標每次加1，y坐標每次要麼加1要麼不變取決於交點的位置。通過判斷中心點位於直線的上方還是下方即可確定y坐標是否需要加1，如下。

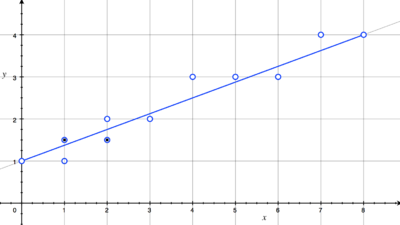
中心點畫線（斜率<1時）

我們可以構造判別式d=F(x+1,y+0.5)=a(x+1)+b(y+0.5)+c：d>0則中點在直線上方，反之在下方。用增量方式計算下一個中點的判別式：
若d>0，則y不變，d1=F(x+2,y+0.5)=a(x+2)+b(y+0.5)+c=d+a;
若d<0，則y+1，d2=F(x+2,y+1.5)=a(x+2)+b(y+1.5)+c=d+(a+b);
初值d0=F(x0+1,y0+0.5)=a(x0+1)+b(y0+0.5)+c=a+0.5b，由於只對d判別正負，可以用2d消除浮點數運算：

x=x0, y=y0, d=2*a+b;
d1=2*a, d2=2*(a+b);

setPixel(x,y);
while(x < x1)
{ 
    if(d < 0)
    {
        x++;
        y++;
        d+=d2;
    }
    else
    {
        x++;
        d+=d1;
    }
    setPixel(x,y);
}

中點畫線法只包含整數變量且沒有乘法運算，適合硬件實現。

還有一種更好的方法Bresenham畫線算法，原理和中點畫線法一樣，不同的是使用交點到上下兩個像素點的距離差作為判別式，同樣采用增量計算，只含整數變量和加法、乘2(位移)運算，不再贅述。

以上便是圖形學裡最簡單的圖形基元——線段的掃描轉換。為了方便底層硬件實現，這些算法都會盡可能的使用整數變量，使用增量計算減少乘除法(或轉化為2的冪次通過位移實現)。按照這種套路不難理解圓、橢圓、多邊形的掃描轉換算法，這裡就不一一探討了。

有了這些圖形基元後，通過變換、投影、裁剪、組合等方式便可以得到更加復雜的圖形。

2.圖形變換

計算機本身只能處理數字信息，各種圖形在計算機系統內也是以數字的形式存在的。為了使被顯示的對象數字化，就需要在被顯示對象所在的空間中定義一個坐標系。

這裡稍微區分一下幾種不同坐標系的概念：

本體坐標系也稱模型坐標系，為將對象數字化而建立的長度單位和坐標軸方向適合被現實對象描述的坐標系。一個復雜模型可能包含很多簡單物體，可以分別對給他們建立一個方便建模的本體坐標系。
用戶坐標系也稱世界坐標系，我們對一個復雜模型建立了很多個本體坐標系，需要在一個大坐標系中將它們組合成一個整體，即世界坐標系。
觀察坐標系，以觀察姿態引入的坐標系。通常約定眼睛的位置為坐標原點，x軸水平向右，y軸豎直向上，z軸離開眼睛射向前方稱為右手系，反之為左手系。
設備坐標系，為了最終將被描述的物體在顯示器上顯示或繪制出來，需要在顯示器屏幕上定義一個二維直角坐標系。而為了達到與具體設備無關而引入的規范化設備坐標系規定坐標范圍為均為0到1。

搞這麼多坐標系，目的其實都是為了方便建模和處理，可見物體從建模到被顯示出來的過程離不開坐標的變換。而為了統一地處理各種坐標變換，需要引入齊次坐標的概念。

齊次坐標表示法就是用n+1維向量表示一個n維向量。n維空間中的一個點(P1,P2,...,Pn)在n+1維空間中的齊次坐標表示為(hP1,hP2,...,hPn,h)。齊次坐標是不唯一的，當h=1時前n個坐標即為原n維空間中的點。

齊次坐標可以表示無窮遠點，例如：(a,b,0)表示二維空間中直線bx-ay=0上的無窮遠點。

應用齊次坐標可以有效地用矩陣運算將點從一個坐標系轉換到另一個坐標系中。

可以理解為低維空間中的某個點p朝著某方向無限延伸到高一維空間中，延伸路徑上的點p1,p2,......都映射到低維空間的p點上，p1,p2......在低維空間中都相當於原始點p。（個人理解。。）

為什麼用齊次坐標就能統一處理變換，從表面上看增加一個維度可以將不同的變換放在同一個矩陣中表示，利用矩陣乘法的結合律也能輕松處理各種變換的組合，至於其中包含的理論原理就不做深入了，可以從變換矩陣的定義中簡單體會一下：

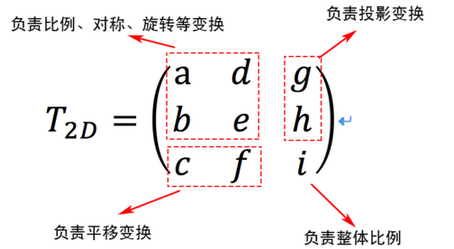
二維齊次坐標變換矩陣形式

將每一行看做齊次坐標，如果是一個單位矩陣，則第一行(1,0,0)表示x軸上的無窮遠點，第二行(0,1,0)表示y軸上的無窮遠點，第三行(0,0,1)則表示坐標原點。所以當二維變換矩陣是單位矩陣時，相當於定義了二維空間中的直角坐標系。

將點p=(x,y,1)變換後的坐標記為p'=(x',y',1)，可得到下面的幾何變換矩陣：

平移變換：x方向移動Tx，y方向移動Ty，則p'=(x+Tx, y+Ty, 1)

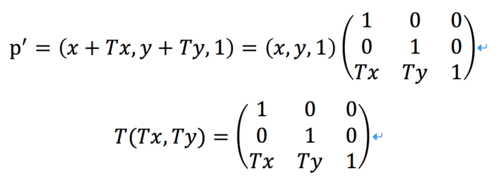
二維平移變換矩陣

比例變換：x方向縮放Sx，y方向縮放Sy，則p'=(x·Sx, y·Sy, 1)

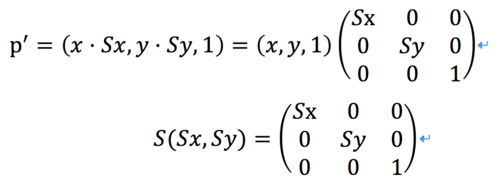
二維比例變換矩陣

旋轉變換：繞坐標原點逆時針旋轉θ，則p'=(x·cosθ-y·sinθ, x·sinθ+y·cosθ, 1)

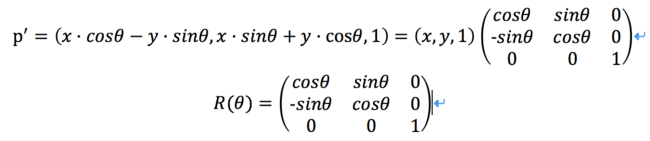
二維旋轉變換矩陣

這些變換都對應3×3的變換矩陣，根據矩陣乘法結合律可以組合出一些復雜的變換，例如繞任意點(x0,y0)旋轉θ：可以先平移讓其位於坐標原點，相對於原點作旋轉變換後在平移回去：

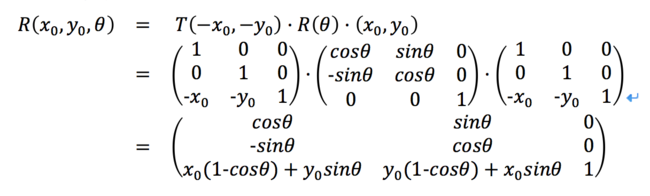
繞點(x0,y0)旋轉θ的變換矩陣

這便是用齊次坐標變換矩陣的方便之處。

類似的，可以推導出三維圖形變換的齊次坐標變換矩陣，這裡不再羅列公式了，我們從蘋果提供的API中簡單了解一下：

/* Homogeneous three-dimensional transforms. */
/* 齊次三維變換 */

/* 齊次三維變換的數據結構，為一個4×4矩陣 */
struct CATransform3D
{
  CGFloat m11, m12, m13, m14;
  CGFloat m21, m22, m23, m24;
  CGFloat m31, m32, m33, m34;
  CGFloat m41, m42, m43, m44;
};

typedef struct CATransform3D CATransform3D;

CATransform3D.h中提供的一些函數：

/* The identity transform: [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]. */
/* 返回一個4×4單位矩陣 */
CA_EXTERN const CATransform3D CATransform3DIdentity
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns true if 't' is the identity transform. */
/* 判斷變換矩陣t是否為單位矩陣 */
CA_EXTERN bool CATransform3DIsIdentity (CATransform3D t)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns true if 'a' is exactly equal to 'b'. */
/* 判斷變換矩陣a和b是否相等 */
CA_EXTERN bool CATransform3DEqualToTransform (CATransform3D a,
    CATransform3D b)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* 下面三個函數用來生成三維平移、比例、旋轉變換矩陣 */

/* Returns a transform that translates by '(tx, ty, tz)':
 * t' =  [1 0 0 0; 0 1 0 0; 0 0 1 0; tx ty tz 1]. 
 * 返回一個三維平移變換矩陣 */
CA_EXTERN CATransform3D CATransform3DMakeTranslation (CGFloat tx,
    CGFloat ty, CGFloat tz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns a transform that scales by `(sx, sy, sz)':
 * t' = [sx 0 0 0; 0 sy 0 0; 0 0 sz 0; 0 0 0 1]. 
 * 返回一個三維比例變換矩陣 */
CA_EXTERN CATransform3D CATransform3DMakeScale (CGFloat sx, CGFloat sy,
    CGFloat sz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns a transform that rotates by 'angle' radians about the vector
 * '(x, y, z)'. If the vector has length zero the identity transform is
 * returned. 
 * 返回一個三維旋轉變換矩陣，旋轉軸為(x,y,z) */
CA_EXTERN CATransform3D CATransform3DMakeRotation (CGFloat angle, CGFloat x,
    CGFloat y, CGFloat z)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* 下面三個函數用來“對變換做變換”，??注意都是左乘 
 * 這裡有點繞，比如對一個平移變換T做縮放變換S，得到的變換
 * 效果是先縮放在平移。我的理解是好比我們看3D電影時，一般
 * 都將3D鏡片放在我們的近視鏡前面，其實是對3D影像先進行處
 * 理，然後通過近視鏡呈現給我們的眼睛，對於影片來說是先進
 * 行3D處理再做近視的變換；而對於眼鏡來說，是它的近視變換
 * 之前被加上了一層3D處理。放在前面的變換才會影響到後面的
 * 變換，即對後面的變換“做了變換”。這裡也是按著蘋果注釋中
 * 的定義強行理解了一波，不知道是不是這樣，還請指教。。 */

/* Translate 't' by '(tx, ty, tz)' and return the result:
 * t' = translate(tx, ty, tz) * t. */
 * 對變換t進行(tx, ty, tz)的平移 */
CA_EXTERN CATransform3D CATransform3DTranslate (CATransform3D t, CGFloat tx,
    CGFloat ty, CGFloat tz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Scale 't' by '(sx, sy, sz)' and return the result:
 * t' = scale(sx, sy, sz) * t. 
 * 對變換t做(sx, sy, sz)的縮放 */
CA_EXTERN CATransform3D CATransform3DScale (CATransform3D t, CGFloat sx,
    CGFloat sy, CGFloat sz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Rotate 't' by 'angle' radians about the vector '(x, y, z)' and return
 * the result. If the vector has zero length the behavior is undefined:
 * t' = rotation(angle, x, y, z) * t. 
 * 對變換t做旋轉angle，旋轉軸為(x,y,z) */
CA_EXTERN CATransform3D CATransform3DRotate (CATransform3D t, CGFloat angle,
    CGFloat x, CGFloat y, CGFloat z)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Concatenate 'b' to 'a' and return the result: t' = a * b. 
 * 組合a,b兩個變換，返回矩陣a*b，相當於先做a變換再做b變換 */
CA_EXTERN CATransform3D CATransform3DConcat (CATransform3D a, CATransform3D b)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Invert 't' and return the result. Returns the original matrix if 't'
 * has no inverse. 
 * 反向變換，相當於對矩陣求逆 */
CA_EXTERN CATransform3D CATransform3DInvert (CATransform3D t)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

3.曲線和曲面

我們開發時經常會用到或見到一個叫貝塞爾曲線的東西，它到底是什麼，能做什麼用，這裡同樣僅從概念上總結下計算機處理曲線和曲面的一些基礎知識以及貝塞爾曲線的原理。

曲線和曲面的表示形式
我們都知道x^2+y^2=r^2 表示一個半徑為r的圓，x^2+y^2=r^2叫做這個圓的方程；我們還可以用x=r·cosθ,y=r·sinθ表示這個圓，稱為它的參數方程。

在空間曲線的參數表示中，曲線上每一個點的坐標均要表示成某個參數t的函數，即：x=x(t), y=y(t), z=z(t)
類似可以得出曲面的參數方程形式：x=x(u,v), y=y(u,v), z=z(u,v)
曲面的一般形式f(x,y,z)=0，而非參數形式的曲線可以定義為兩個柱面的交線
1963年美國波音飛機公司的Fe

rguson首先提出將曲線曲面表示為參數的向量方程的方法。在此之前的畫法幾何和機械制圖中，很難對自由型曲線進行清晰的表示。

插值和逼近

計算機中通常事先給定一些離散點（稱為型值點），由這些點得出曲線的方法大體分為兩類：一類要求曲線通過這些離散點，稱為插值；另一類用這些點形成控制多邊形來控制形狀，稱為逼近。
當型值點太多時，構造插值函數通過所有型值點是很困難的；或者當型值點本身帶有誤差時也沒有必要尋找一個插值函數通過所有型值點，此時我們往往希望構造一條曲線在某種意義上逼近這些型值點。由型值點求插值或逼近曲線曲面的問題稱為曲線或曲面的擬合。

貝塞爾曲線(Bézier curve)

法國雷諾(Renault)汽車公司的工程師Bézier於1971年發表了一種有控制多邊形定義曲線的方法。設計員只要移動控制點就可以方便的修改曲線的形狀，而且形狀變化完全在意料之中，漂亮的解決了整體形狀控制的問題。

貝塞爾曲線的定義其實並不復雜，我們用P0,P1,...,Pn表示給定的n+1個型值點（為什麼是n+1，因為至少要有兩個點才能構造線。。），而貝塞爾曲線的實質就是用n次多項式函數對這n+1個點進行混合：

貝塞爾曲線的參數定義

所以，n次貝塞爾曲線其實就是一條n次參數多項式曲線。由於組合多項式的特殊性，貝塞爾曲線也有很多有意思的性質，比如：

起點和終點處的切線與控制多邊形的第一和最後一邊重合；
某一起點或終點的r階導數由起點或終點以及它們的r個鄰近的控制點決定，事實上正是由該性質推導出的貝塞爾曲線；
對稱性：從起點出發和從終點出發得到同一條曲線。
分割遞推性：由P0,P1,...,Pn所確定的n次貝塞爾曲線在點t的值可以由點P0,P1,...,Pn-1所確定的n-1次貝塞爾曲線在點t的值，與由點P1,P2,...,Pn所確定的n-1次貝塞爾曲線在點t的值通過線性組合求得：