概述

---

又研究了將近兩個星期的3D圖形到了我最想研究的地方了,因為歐拉角與四元數的原因導致OpenGL ES的研究進度變緩,研究完這一塊,我將教大家如何使用OpenGL ES做一個自轉加公轉的正立方體.效果如下.

方向、方位與角位移的區別

---

在說矩陣、歐拉角與四元數三種與角位移的關系之前,我們先來說說 方向、方位與角位移的區別.

在現實生活中,我們很少區分"方向"和"方位"的區別(非路癡觀點),比如一個朋友來看望你,但是他可能在某一個公交站下車了,你去接他,但是找不到他,你急忙給他來一個電話"兄弟,你在哪個方向呢?"或者說是"兄弟,你在哪個方位呢?",如果不細細品味這兩句話,其實感覺差異不是太大.通過一痛電話的扯,然後你們成功的面基了,但是你們卻並不會在意"方向"和"方位"的區別.那麼在幾何中,這兩者到底有什麼差異呢?

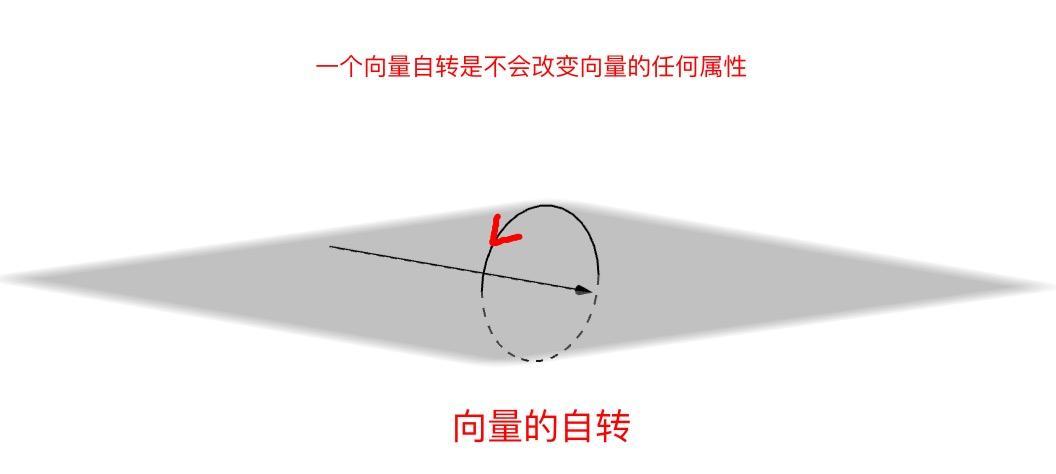
這裡我就盜用一下書上的例子,比如一個向量如果沿著自己的方向選擇是不會改變自身任何屬性的,如下圖所示,因為向量是只有方向沒有方位的.

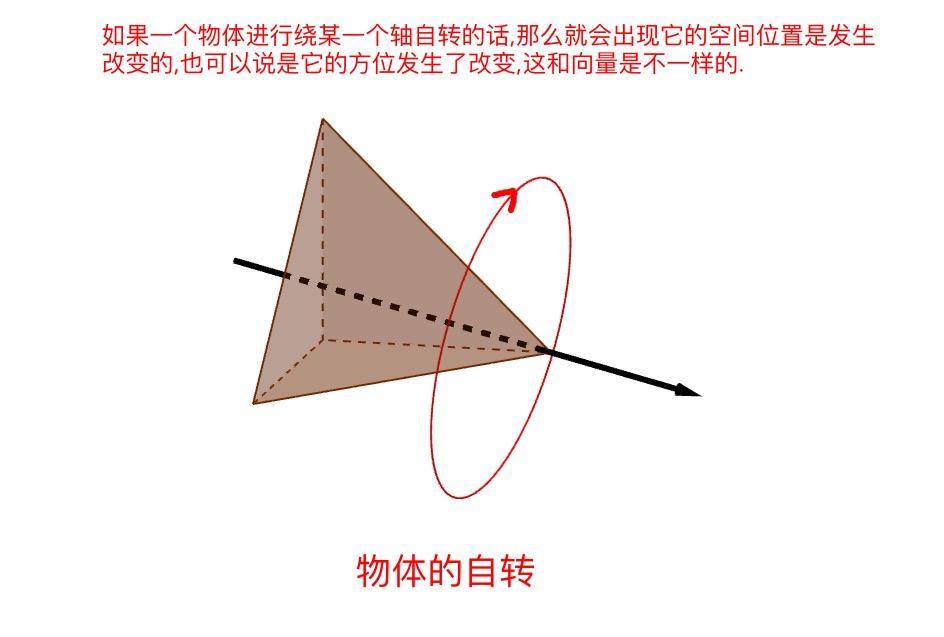
那麼對於一個物體,情況卻是不一樣的,一個物體如果朝向某一個方向的時候,然後自轉,那麼這個物體是會發生空間上的改變的,如下圖一個錐體的自轉,那麼它的空間位置是發生改變的,也就是錐體的方位發生了改變了.

上面讓我們對物體的方向和方位的區別有了一個大體上的了解,那麼我們在空間中如何描述一個方位呢?這就需要使用到角位移了.

我們先說一個類似的例子,我們該如何描述空間中一個物體的位置呢?必須要把物體放在特定的坐標系中(好像很生澀).比如,如果我們說在一個坐標系中,有一個點是[1,1,1],那麼你會非常輕易的想到了這個點在空間中的位置.描述空間位置其實就是描述相對於給定參考點(坐標原點)的位移.

其實,描述一個物體的方位是一樣的,我們是不可能憑空描述一個物體的方位,我盟需要一個已知方位的參考量,通過這個參考量的旋轉得到當前方位,那麼旋轉的量就叫做角位移.通過概念我們知道,角位移就是用來描述方位的,類似於速度就是用來描述物體運動快慢的一樣.當然了,這裡我要聲明的一點就是雖然角位移是用來描述方位的,但是兩者是不同的.例如,我們可以這麼說,一個物體的方位是如何如何的;一個物體是通過某個已知方位經過角位移XXX旋轉得到.所以說,方位是用來描述一個單一的"狀態".但是角位移是用來描述兩個狀態之間的差異.

那麼,我們在實際中如何描述方位與角位移呢?具體而言,我們使用矩陣和四元數來表示"角位移",用歐拉角來表示方位.接下來,我們逐一介紹一下.

使用矩陣表示角位移

---

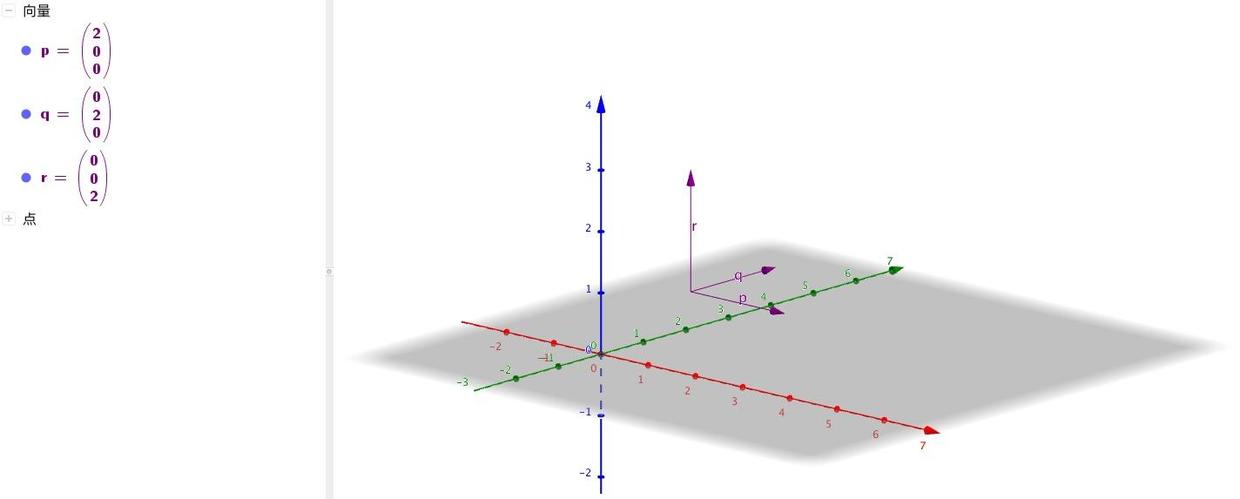
在3D環境中,描述坐標系中方位的方式就是列出這個坐標系的基向量,當然了,這些基向量是用其他表示的,並不是它本身的基向量,比如當前轉換完成的坐標系的三個基向量p [1,0,0] q[0,1,0] r[0,0,1],這是使用本身的坐標系表示,如果放在其他坐標系中表示當前的三個基向量可能就會發生改變.這是因為參照點選擇的不同.至於基向量是如何改變的就需要在3D圖形:矩陣與線性變換說過的旋轉矩陣的相關知識了.這個就不過多的解釋了.比如下圖,由向量p,q,r組建的新的坐標系用原來的坐標系表示確實如圖右邊所示.

其實對於我們開發來說,我們只需要知道方位是可以使用3X3矩陣來表示的.矩陣表示的是轉換後的基向量即可.接下來我們說一下使用矩陣來表示角位移有什麼樣的優勢和缺點.我就直接拿書上所講的了,各位看官莫怪莫怪.

使用矩陣表示角位移的優勢

• 可以立即進行向量的旋轉.後面使用四元數進行空間變化其實是和使用對應的矩陣的空間變化的效果是一樣的.

• 矩陣的形式被圖形API所使用.這一點我們從OpenGL ES 就可以看出來了,無需過多解釋了.

• 多個角位移連接.我們知道使用矩陣進行空間變換是可以連續進行多個的.那麼角位移也是一樣的.

• 矩陣的逆.這個比較好理解,如果我們進行了一次旋轉變換(也就是空間方位的變化),那麼如何回到原來的方位呢,只要再乘上一次矩陣的逆即可,前面說過矩陣的逆是有這樣的功能的.

使用矩陣表示角位移的缺點

• 矩陣可能占有更多內存.這其實是由比較性的,這種比較是要與歐拉角做比較,與歐拉角比較矩陣所占的內存將會更多.

• 難以使用.這個確實是,你想想,如果現在你要x軸旋轉80°,你還要想想它對應的向量是多少.一痛計算之後,才能得到對用的值,後面直接看到這個矩陣的時候還要接著計算,看看它是如何變換的.這樣使用起來是不是非常的惡心?

• 並非所有矩陣都能描述方位.這一點,我將單獨寫一篇來討論這個問題.現在還不是太了解,見諒.

當然了,我們使用矩陣來表示角位移只是作為了解而已,接下來,我們看一下如何使用歐拉角表示方位的.

歐拉角表示方位與萬向鎖問題

---

很多人在大學中可能會接觸到矩陣,但是歐拉角可能是接觸的比較少,最少作為一個學物理的我是這樣的.一開始覺得歐拉角比較難理解,但是看了3D圖形之後,發現用歐拉角表示方位將會比矩陣更加的直觀而且易於使用.下面我們就看一下歐拉角相關的知識.(下面的基本概念跟書上的差不多,因為我覺得書上寫個就很好了,所以我就沒有再次總結,所以只是寫了一遍.)

首先,歐拉角的基本思想是將角位移分解為繞三個互相垂直軸的三個旋轉組成的序列.那麼這個三個互相垂直的軸是如何定義的呢?其實任意三個軸和任意順序都是可以的,但是最常用的就是使用笛卡爾坐標系並且按照一定順序組成的旋轉序列.最常用的約定,就是所謂的"heading-pitch-bank"約定,在這個系統中,一個方位被定義為heading角,一個pitch角,一個bank角.其中,在左手坐標系中,我們把heading角定義為繞y軸旋轉量,pitch角為繞x軸旋轉量,bank角為繞z軸旋轉量.旋轉法則遵守左手法則(具體請參考3D圖形:矩陣與線性變換中的旋轉模塊).它的基本思想是讓物體開始於"標准"方位,就是物體坐標軸和慣性坐標軸對齊.讓物體做heading、pitch、bank旋轉之後達到最終的空間方位.

例如下圖一個錐體,一開始它自身坐標軸與慣性坐標軸是一致.

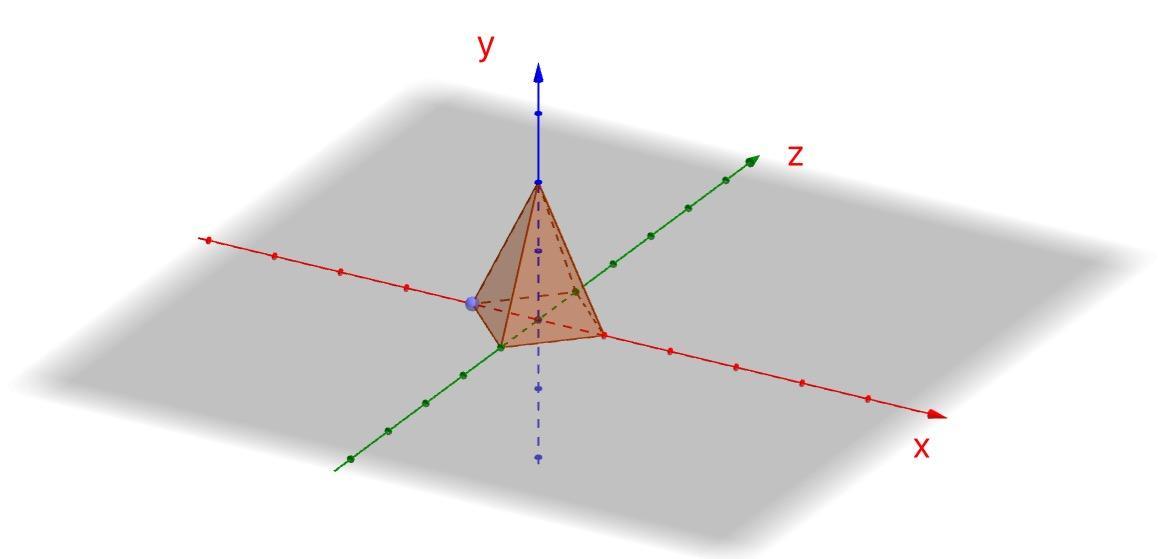
然後我把heading角設置為45°.根據左手法則(通常使用,但是決定每個旋轉的正方向不一定要准守右手或者左手定則),它是會做順時針旋轉.

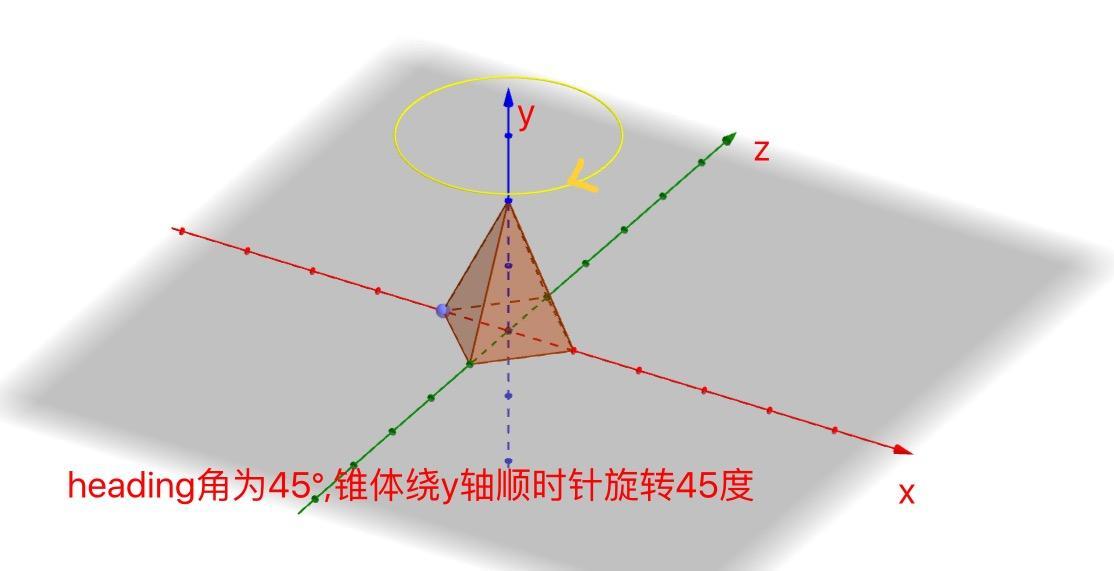
接著物體的坐標系就發生如下的改變了.錐體的自身坐標軸不再與慣性坐標軸一致,x,z軸都發生了對應的改變.當然了,物體的空間方位也發生了對應的改變.

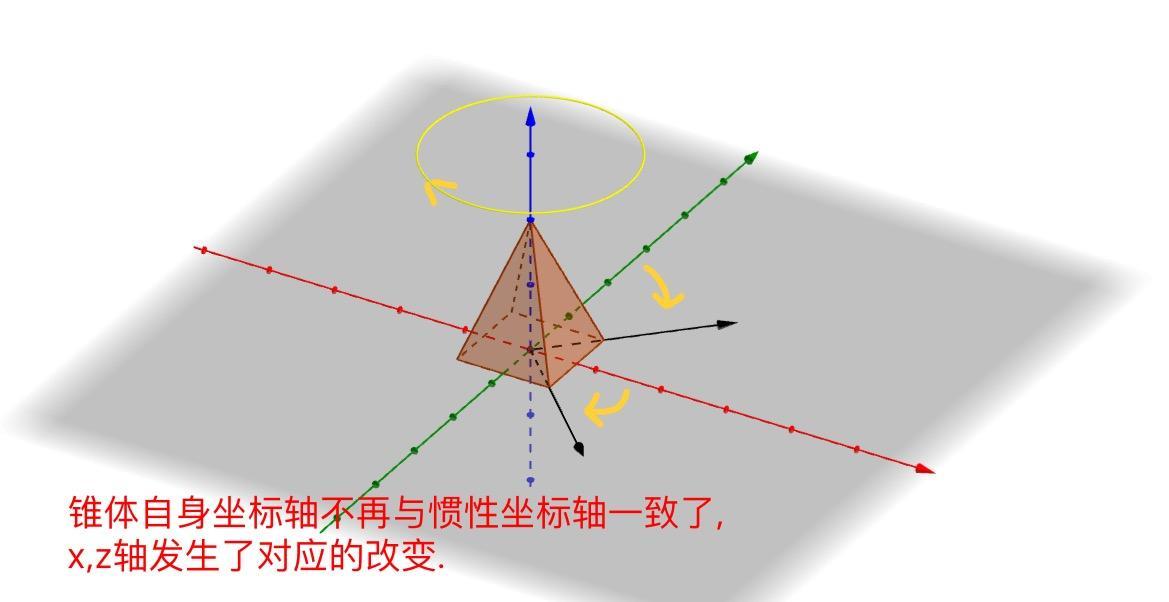
然後接下來就是pitch、bank旋轉,分別是繞x軸旋轉和z軸旋轉,跟heading旋轉是類似的,最後得到錐體的最終的空間方位.這裡需要注意的是不管是 heading旋轉、 pitch旋轉還是bank旋轉,旋轉的坐標軸都是自身的坐標軸!不是慣性坐標軸!

上面,看完了"heading-pitch-bank"約定系統是如何做空間方位的旋轉改變的,接下來,我們來瞅瞅關於歐拉角的其他約定.

• "heading-pitch-bank"約定系統是有多個名字的,其中的有一組叫做"roll-pitch-yaw",其中roll等同於bank,yaw等價於heading.我們知道"heading-pitch-bank"約定是讓方位從慣性坐標系到最終的物體自身坐標系,但是"roll-pitch-yaw"約定卻是剛好相反.它是從最終的物體坐標系到最開始的慣性坐標系的旋轉變換.

• 任意的三個軸都能作為旋轉軸,但是使用笛卡爾坐標軸是最有意義的,這句話我就不過多解釋了,我們在上面的例子中已經深有體會了.

• 決定每一個旋轉的正方向不一定必須遵守左手或者右手法則,這樣遵守只是習慣而已.

• 旋轉是可以以不同的順序進行的, "heading-pitch-bank"約定系統只是更比較如何人的習慣而已.因為一個物體放在一個水平面上,如果進行旋轉操作的話,我們首先想到的是物體按照垂直軸進行旋轉操作.也就是heading旋轉.

上面我們對歐拉角的接下來,我們看一下歐拉角的優點和缺點.透露一點,其實歐拉角的缺點就是引起萬向鎖的原因.

歐拉角表示方位的優點

• 歐拉角使用起來非常的簡單方便,它比四元數以及矩陣更加的生動形象.因為歐拉角使用都是角度,對於人來說旋轉還是使用角度比較直觀.

• 最簡潔的表達方式.在3D中,歐拉角用3個數就可以表達方位,四元數則要用4個數,而矩陣是最多的,需要9個數.

• 任意三個數都是合法的,任意的三個數都是能構成合法的歐拉角,矩陣和四元數可不一定是這樣的.

歐拉角表示方位的缺點

• 給定的方位表達方式不唯一.我們雖然說任意三個數組成的歐拉角都是合法的,但是比如heading旋轉360°和選擇720°,物體的方位是一直的,雖然歐拉角的數值是發生了改變的.

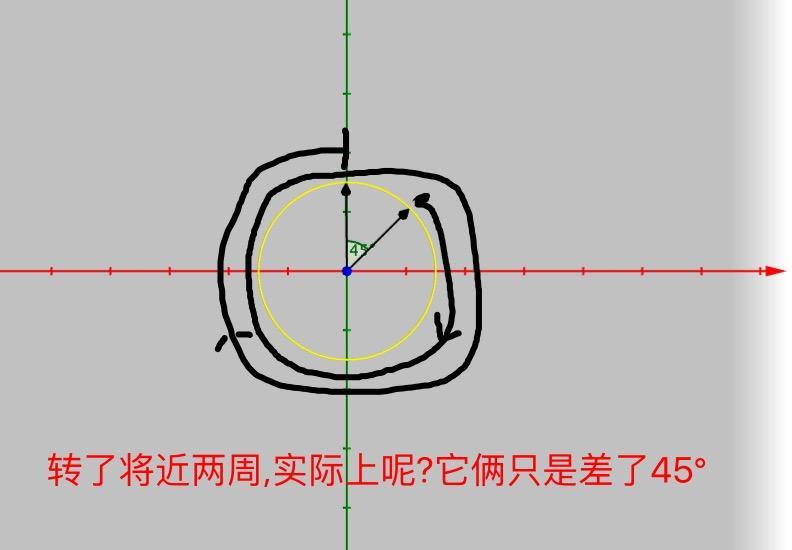
• 兩個角度求插值非常的困難.比如方位A的heading角度為720°,方位B的角度為45°.那麼heading值差了多少呢?沒錯就是45°,因為720°就是旋轉了兩周而已,但是實際上我們操作的時候需要選擇將近兩周.如下圖所示.

萬向鎖問題

其實是使用歐拉角會出現一個非常有趣的現象,那就是萬向鎖,我們看一下"heading-pitch-bank"系統這個系統中,如果pitch角度為±90°,那麼就出事了,會出現什麼問題呢?heading角與bank角如果相同,那麼你會發現物體最終的方位是一致的,這怎麼可能,這就比較尴尬了,其實類似於這種旋轉pitch角度為±90°中,物體是缺失一個旋轉軸的.也就是說,當pitch角度為±90°,那麼bank是0.只有heading一個旋轉軸起作用,是不是懵圈了?沒問題,下面我要分享一個視頻,我覺得這個視頻會比文字更加生動形象,請對照上面的文字自行研究.

歐拉旋轉—萬向節鎖視頻傳送門????

四元數與復數

---

看完使用矩陣和歐拉角表示方位.接下來,我們就看一下四元數,四元數一個新的概念出現在我的眼前的時候我在想,他否是因為有四個數才叫四元數,確實,四元數實際是一個標量分量和一個3D向量分量組成用來表示方位.四元數的兩種記法如下所示:[ω,ν],[ω,(x,y,z)].
復數,真心好久沒用了.高中的時候我們就開始接觸簡單的復數了,現在簡單說一下復數,其實我也順道復習一下了.
首先,復數的形式為a+bi,其中i?=-1,a稱作實部(實數部分),b稱作虛部(虛數部分).對於復數的運算,我們主要說說復數的模,復數的模可以很好的表示2D中的旋轉變換,我們先看看前面說到過的2D環境中的旋轉矩陣.

然後,我們再看一下,一個示例,假設一個復數v = (x,y)旋轉θ度得到v',如下圖所示.

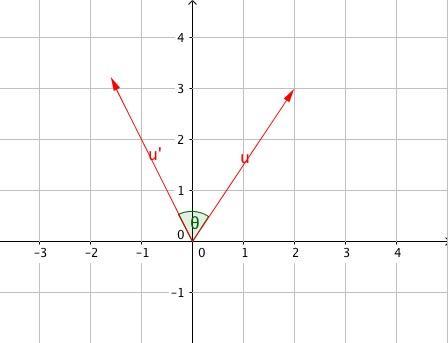
為了完成此次的旋轉,我們需要引入第二個復數 q = (cosθ,sinθ),現在旋轉之後的復數v'就可以使用復數的乘法計算出來了.計算過程如下所示.
v = x +yi
q = cosθ +isinθ
v' = vq = (x +yi)(cosθ +isinθ) = (xcosθ-ysinθ)+(xsinθ+ycosθ)i
跟上面的2D環境中旋轉矩陣效果是一樣的.只是形式不相同而已.

上面說了這麼一大堆,那麼到底四元數和復數有著怎樣的關系呢?其實一個四元數[w,(x,y,z)]定義了復數w +xi +yj +zk,也就是說一個四元數是包含著一個實部和三個虛部.
其實四元數的出現也是有故事的,我直接把書上搬過來,當做在枯燥的學習中的一個輕松時刻吧(實際上,然並卵????????????),愛爾蘭的數學家哈密爾頓其實一直想把復數復數從2D擴展到3D,一開始他認為,3D中的復數應該有一個實部和兩個虛部,然後他沒有創造出這種一個實部兩個虛部有意義的復數.1843年,在他去演講的路上他突然意識到應該有三個虛部而不是兩個虛部.他把這種新復數類型行者的等式刻在了Broome橋上.這樣四元數就誕生了.等式如下所示.
i? = j? = k? = -1
ij = k,ji = -k
jk = i,kj = -i
ki = j,ik = -j

四元數和軸-角對

---

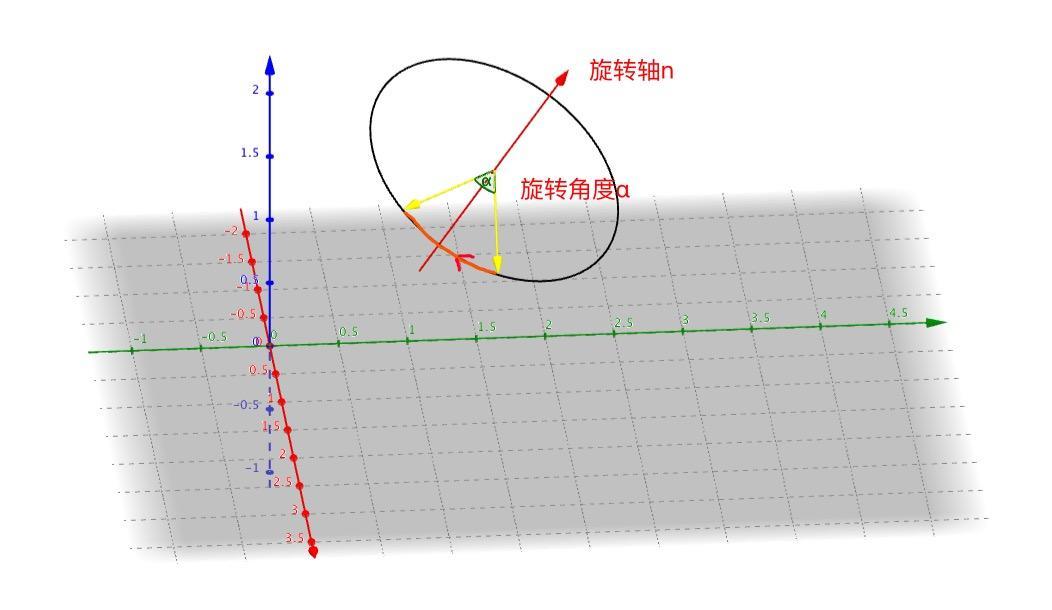
我們已經知道了矩陣和歐拉角的情況,現在我們就看一下四元數是如何表示角位移的.在3D環境中任意的一個角位移都可以理解為繞某個軸旋轉一定的角度,在3D圖形:矩陣與線性變換這個裡面曾經說過一個3D中繞任意軸旋轉的公式(還記得當初那個驗證過程嗎,愣是搞了一天????,具體驗證過程就不說了,請查看原來的文章).公式如下所示.其中,θ代表著旋轉角度,n代表著旋轉軸.因此軸-角對(n,θ)定義了一個角位移:繞n指定的軸旋轉θ角.

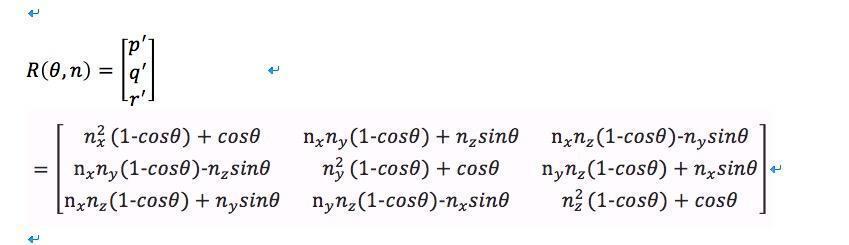
四元數的解釋其實就是角位移的軸-角對方式,但是呢,n和θ並不是直接放入到四元數中的.它們的形式如下所示.

q = [ cos (θ/2)   sin(θ/2)n ]
=[ cos (θ/2)  ( sin(θ/2)nx    sin(θ/2)ny     sin(θ/2)nz ) ]

那麼問題來了,為什麼不直接放入四元數中呢?這是有原因的,這個原因,我將會在下一篇四元數的相關運算中來說明一下.現在只要知道四元數的解釋其實就是角位移的軸-角對方式即可.

結束

---

自己寫完這篇文章總算是對矩陣、歐拉角、四元數、角位移、方位有了一個大體的了解了.整體下來發現真心枯燥的,但是還是堅持了下來了,希望小伙伴也能堅持看完,不懂的或者有疑問可以與騷棟一起探討.3D圖像下一篇我將接著研究本篇的四元數,不過是與四元數的運算相關的知識.希望大家持續關注.

最後還是要附上<<3d數學基礎>>的pdf版的傳送門.

--> <<3d數學基礎>>傳送門????