背景

識別二維碼的項目數不勝數，每次都是開箱即用，方便得很。

這次想用 OpenCV 從零識別二維碼，主要是溫習一下圖像處理方面的基礎概念，熟悉 OpenCV 的常見操作，以及了解二維碼識別和編碼的基本原理。

作者本人在圖像處理方面還是一名新手，采用的方法大多原始粗暴，如果有更好的解決方案歡迎指教。

QRCode

二維碼有很多種，這裡我選擇的是比較常見的 QRCode 作為探索對象。QRCode 全名是 Quick Response Code，是一種可以快速識別的二維碼。

尺寸

QRCode 有不同的 Version ，不同的 Version 對應著不同的尺寸。將最小單位的黑白塊稱為 module ，則 QRCode 尺寸的公式如下：

Version V = ((V-1)*4 + 21) ^ 2 modules

常見的 QRCode 一共有40種尺寸：

• Version 1 : 21 * 21 modules

• Version 2 : 25 * 25 modules

• …

• Version 40: 177 * 177 modules

分類

QRCode 分為 Model 1、Model 2、Micro QR 三類：

• Model 1 ：是 Model 2 和 Micro QR 的原型，有 Version 1 到 Version 14 共14種尺寸。

• Model 2 ：是 Model 1 的改良版本，添加了對齊標記，有 Version 1 到 Version 40 共40種尺寸。

• Micro QR ：只有一個定位標記，最小尺寸是 11*11 modules 。

組成

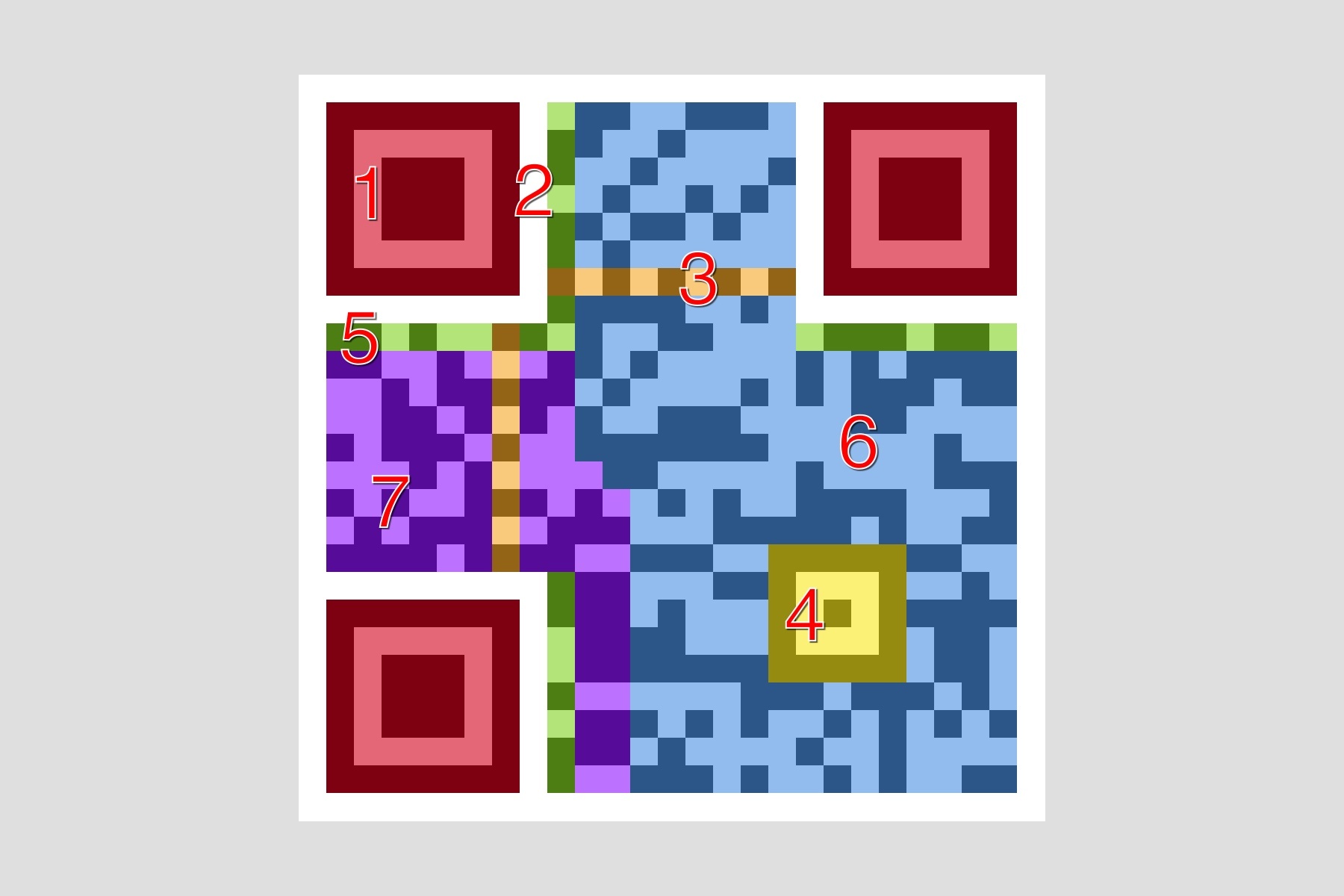
QRCode 主要由以下部分組成：

• 1 - Position Detection Pattern：位於三個角落，可以快速檢測二維碼位置。

• 2 - Separators：一個單位寬的分割線，提高二維碼位置檢測的效率。

• 3 - Timing Pattern：黑白相間，用於修正坐標系。

• 4 - Alignment Patterns：提高二維碼在失真情況下的識別率。

• 5 - Format Information：格式信息，包含了錯誤修正級別和掩碼圖案。

• 6 - Data：真正的數據部分。

• 7 - Error Correction：用於錯誤修正，和 Data 部分格式相同。

具體的生成原理和識別細節可以閱讀文末的參考文獻，比如耗子叔的這篇《二維碼的生成細節和原理》。

由於二維碼的解碼步驟比較復雜，而本次學習重點是數字圖像處理相關的內容，所以本文主要是解決二維碼的識別定位問題，數據解碼的工作交給第三方庫（比如 ZBAR）完成。

OpenCV

在開始識別二維碼之前，還需要補補課，了解一些圖像處理相關的基本概念。

contours

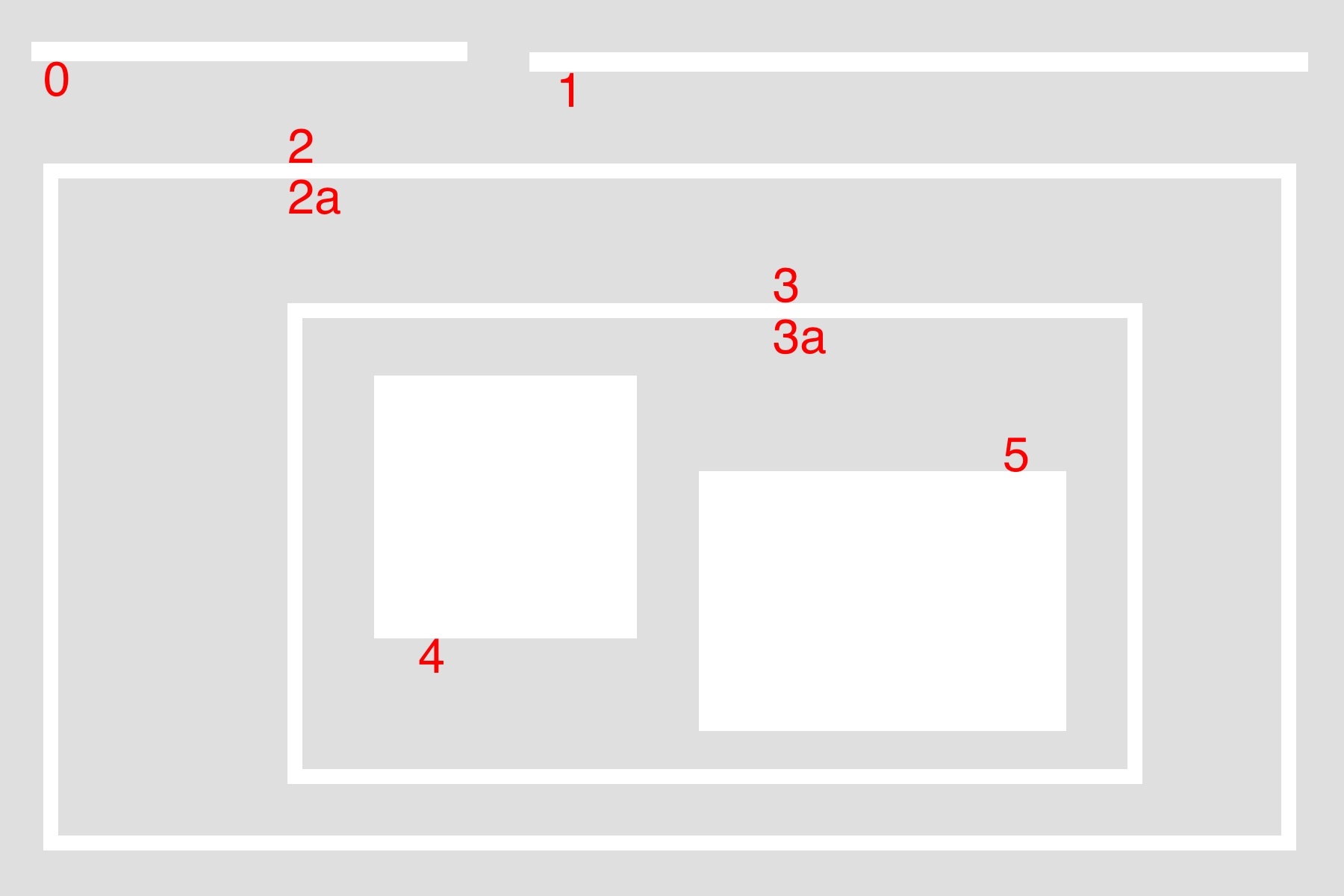
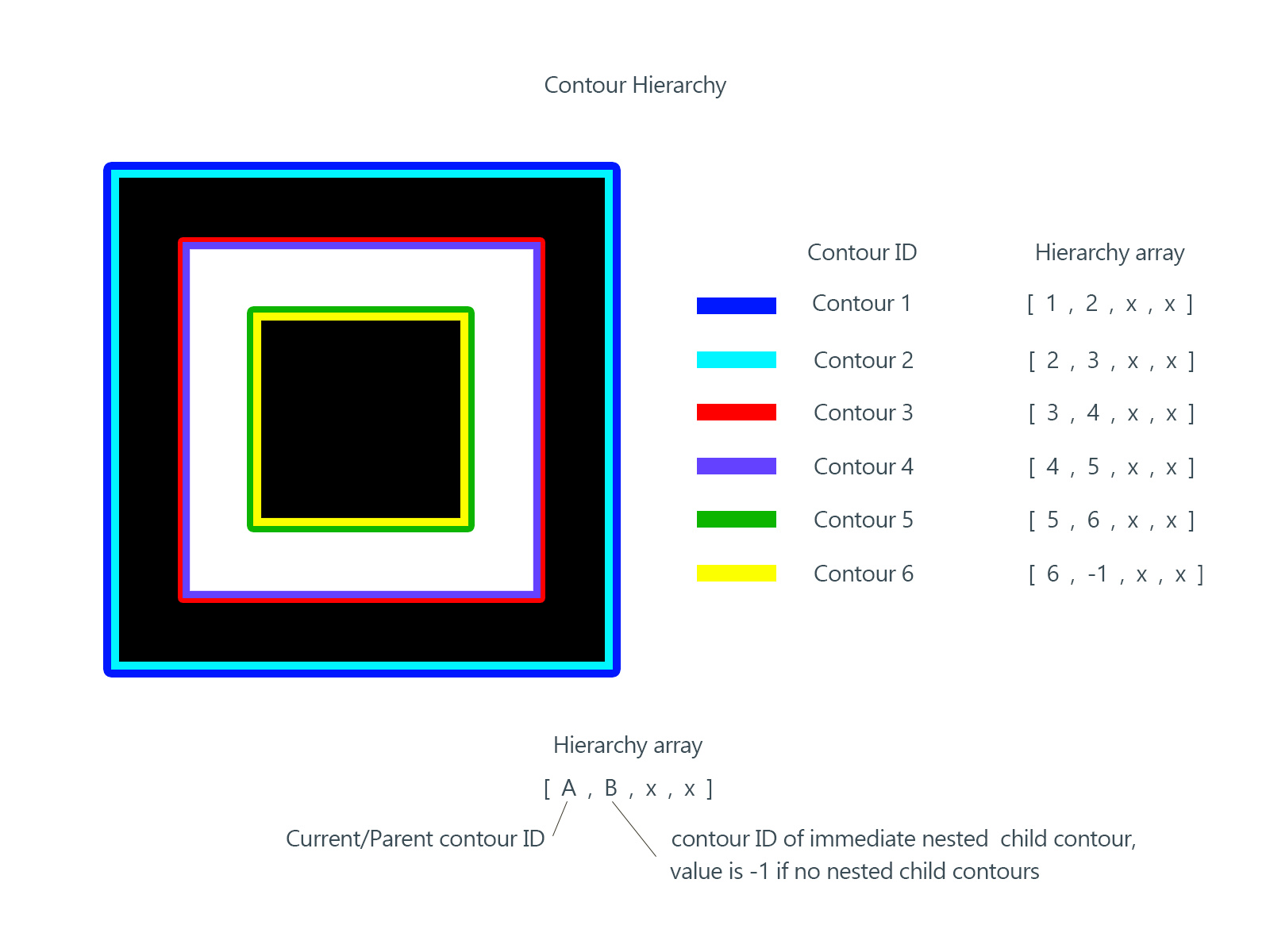
輪廓（contour）可以簡單理解為一段連續的像素點。比如一個長方形的邊，比如一條線，比如一個點，都屬於輪廓。而輪廓之間有一定的層級關系，以下圖為例：

主要說明以下概念：

• external & internal：對於最大的包圍盒而言，2 是外部輪廓（external），2a 是內部輪廓（internal）。

• parent & child：2 是 2a 的父輪廓（parent），2a 是 2 的子輪廓（child），3 是 2a 的子輪廓，同理，3a 是 3 的子輪廓，4 和 5 都是 3a 的子輪廓。

• external | outermost：0、1、2 都屬於最外圍輪廓（outermost）。

• hierarchy level：0、1、2 是同一層級（same hierarchy），都屬於 hierarchy-0 ，它們的第一層子輪廓屬於 hierarchy-1 。

• first child：4 是 3a 的第一個子輪廓（first child）。實際上 5 也可以，這個看個人喜好了。

在 OpenCV 中，通過一個數組表達輪廓的層級關系：

[Next, Previous, First_Child, Parent]

• Next：同一層級的下一個輪廓。在上圖中， 0 的 Next 就是 1 ，1 的 Next 就是 2 ，2 的 Next 是 -1 ，表示沒有下一個同級輪廓。

• Previous：同一層級的上一個輪廓。比如 5 的 Previous 是 4， 1 的 Previous 就是 0 ，0 的 Previous 是 -1 。

• First_Child：第一個子輪廓，比如 2 的 First_Child 就是 2a ，像 3a 這種有兩個 Child ，只取第一個，比如選擇 4 作為 First_Child 。

• Parent：父輪廓，比如 4 和 5 的 Parent 都是 3a ，3a 的 Parent 是 3 。

關於輪廓層級的問題，參考閱讀：《Tutorial: Contours Hierarchy》

findContours

了解了 contour 相關的基礎概念之後，接下來就是在 OpenCV 裡的具體代碼了。

findContours 是尋找輪廓的函數，函數定義如下：

cv2.findContours(image, mode, method) → image, contours, hierarchy

其中：

• image：資源圖片，8 bit 單通道，一般需要將普通的 BGR 圖片通過 cvtColor 函數轉換。

• mode：邊緣檢測的模式，包括：

  • CV_RETR_EXTERNAL：只檢索最大的外部輪廓（extreme outer），沒有層級關系，只取根節點的輪廓。

  • CV_RETR_LIST：檢索所有輪廓，但是沒有 Parent 和 Child 的層級關系，所有輪廓都是同級的。

  • CV_RETR_CCOMP：檢索所有輪廓，並且按照二級結構組織：外輪廓和內輪廓。以前面的大圖為例，0、1、2、3、4、5 都屬於第0層，2a 和 3a 都屬於第1層。

  • CV_RETR_TREE：檢索所有輪廓，並且按照嵌套關系組織層級。以前面的大圖為例，0、1、2 屬於第0層，2a 屬於第1層，3 屬於第2層，3a 屬於第3層，4、5 屬於第4層。

• method：邊緣近似的方法，包括：

  • CV_CHAIN_APPROX_NONE：嚴格存儲所有邊緣點，即：序列中任意兩個點的距離均為1。

  • CV_CHAIN_APPROX_SIMPLE：壓縮邊緣，通過頂點繪制輪廓。

drawContours

drawContours 是繪制邊緣的函數，可以傳入 findContours 函數返回的輪廓結果，在目標圖像上繪制輪廓。函數定義如下：

Python: cv2.drawContours(image, contours, contourIdx, color) → image

其中：

• image：目標圖像，直接修改目標的像素點，實現繪制。

• contours：需要繪制的邊緣數組。

• contourIdx：需要繪制的邊緣索引，如果全部繪制則為 -1。

• color：繪制的顏色，為 BGR 格式的 Scalar 。

• thickness：可選，繪制的密度，即描繪輪廓時所用的畫筆粗細。

• lineType: 可選，連線類型，分為以下幾種：

  • LINE_4：4-connected line，只有相鄰的點可以連接成線，一個點有四個相鄰的坑位。

  • LINE_8：8-connected line，相鄰的點或者斜對角相鄰的點可以連接成線，一個點有四個相鄰的坑位和四個斜對角相鄰的坑位，所以一共有8個坑位。

  • LINE_AA：antialiased line，抗鋸齒連線。

• hierarchy：可選，如果需要繪制某些層級的輪廓時作為層級關系傳入。

• maxLevel：可選，需要繪制的層級中的最大級別。如果為1，則只繪制最外層輪廓，如果為2，繪制最外層和第二層輪廓，以此類推。

moments

矩（moment）起源於物理學的力矩，最早由阿基米德提出，後來發展到統計學，再後來到數學進行歸納。本質上來講，物理學和統計學的矩都是數學上矩的特例。

物理學中的矩表示作用力促使物體繞著支點旋轉的趨向，通俗理解就像是擰螺絲時用的扭轉的力，由矢量和作用力組成。

數學中的矩用來描述數據分布特征的一類數字特征，例如：算術平均數、方差、標准差、平均差，這些值都是矩。在實數域上的實函數 f(x) 相對於值 c 的 n 階矩為：

常用的矩有兩類：

• 原點矩（raw moment）：相對原點的矩，即當 c 為 0 的時候。1階原點矩為期望，也成為中心。

• 中心矩（central moment）：相對於中心點的矩，即當 c 為 E(x) 的時候。1階中心矩為0，2階中心矩為方差。

到了圖像處理領域，對於灰度圖（單通道，每個像素點由一個數值來表示）而言，把坐標看成二維變量 (X, Y)，那麼圖像可以用二維灰度密度函數 I(x, y) 來表示。

簡單來講，圖像的矩就是圖像的像素相對於某個點的分布情況統計，是圖像的一種特征描述。

raw moment

圖像的原點矩（raw moment）是相對於原點的矩，公式為：

對於圖像的原點矩而言：

• M₀₀ 相當於權重系數為 1 。將所有 I(x, y) 相加，對於二值圖像而言，相當於將每個點記為 1 然後求和，也就是圖像的面積；對於灰度圖像而言，則是圖像的灰度值的和。

• M₁₀ 相當於權重為 x 。對二值圖像而言，相當於將所有的 x 坐標相加。

• M₀₁ 相當於權重為 y 。對二值圖像而言，相當於將所有的 y 坐標相加。

• 圖像的幾何中心（centroid）等於 (M₁₀ / M₀₀ , M₀₁ / M₀₀)。

central moment

圖像的中心矩（central moment）是相對於幾何中心的矩，公式為：

可以看到，中心矩表現的是圖像相對於幾何中心的分布情況。一個通用的描述中心矩和原點矩關系的公式是：

中心矩在圖像處理中的一個應用便是尋找不變矩（invariant moments），這是一個高度濃縮的圖像特征。

所謂的不變性有三種，分別對應圖像處理中的三種仿射變換：

• 平移不變性（translation invariants）：中心矩本身就具有平移不變性，因為它是相對於自身的中心的分布統計，相當於是采用了相對坐標系，而平移改變的是整體坐標。

• 縮放不變性（scale invariants）：為了實現縮放不變性，可以構造一個規格化的中心矩，即將中心矩除以 (1+(i+j)/2) 階的0階中心矩，具體公式見 《Wiki: scale invariants》。

• 旋轉不變性（rotation invariants）：通過2階和3階的規格化中心矩可以構建7個不變矩組，構成的特征量具有旋轉不變性。具體可以看 《Wiki: rotation invariants》。

Hu moment 和 Zernike moment 之類的內容就不繼續展開了，感興趣的可以翻閱相關文章。

OpenCV + QRCode

接下來就是將 QRCode 和 OpenCV 結合起來的具體使用了。

初步構想的識別步驟如下：

• 加載圖像，並且進行一些預處理，比如通過高斯模糊去噪。

• 通過 Canny 邊緣檢測算法，找出圖像中的邊緣

• 尋找邊緣中的輪廓，將嵌套層數大於 4 的邊緣找出，得到 Position Detection Pattern 。

• 如果上一步得到的結果不為 3 ，則通過 Timing Pattern 去除錯誤答案。

• 計算定位標記的最小矩形包圍盒，獲得三個最外圍頂點，算出第四個頂點，從而確定二維碼的區域。

• 計算定位標記的幾何中心，連線組成三角形，從而修正坐標，得到仿射變換前的 QRCode 。

在接下來的內容裡，將會嘗試用 OpenCV 識別下圖中的二維碼：

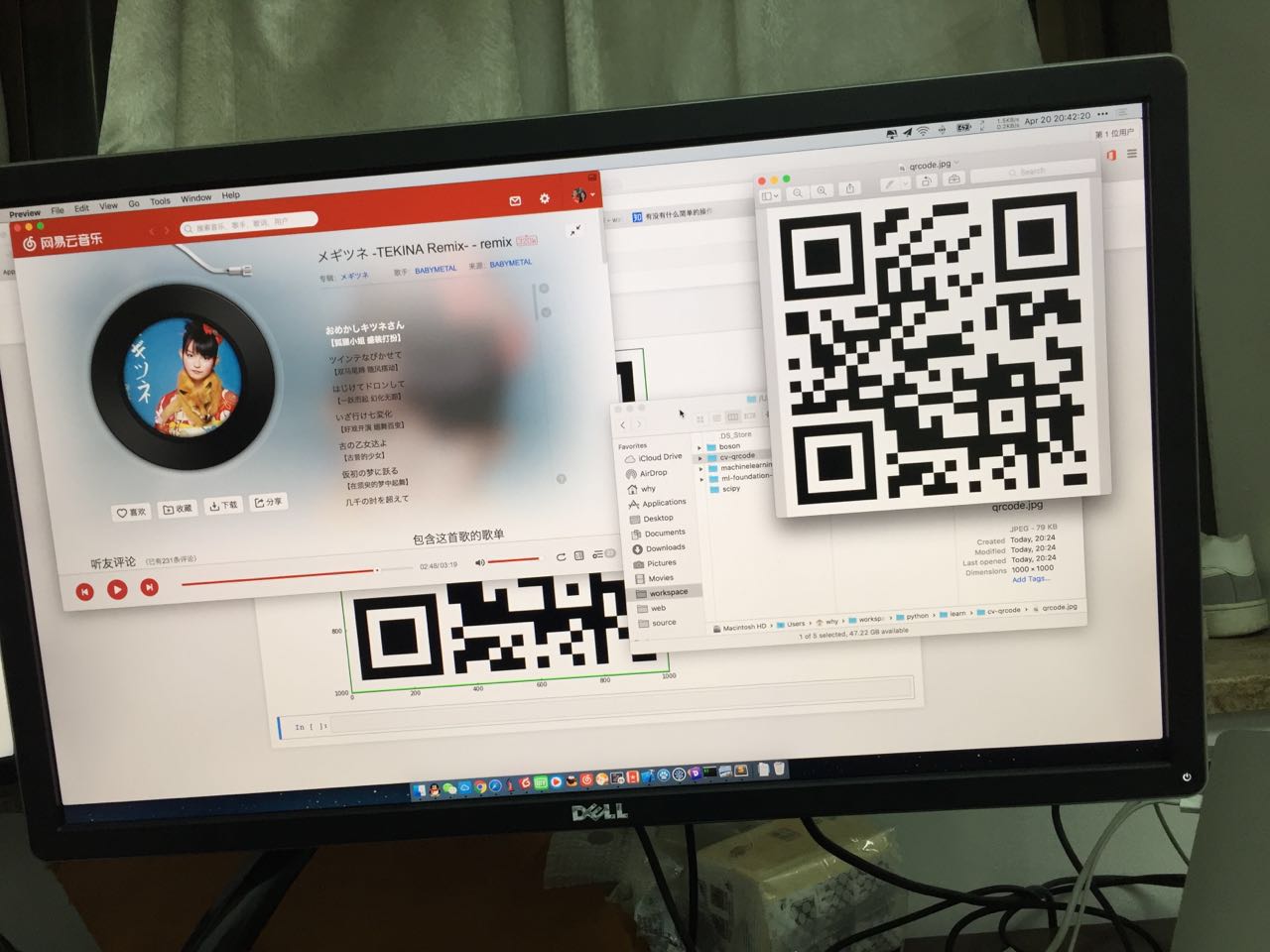
加載圖像

首先加載圖像，並通過 matplotlib 顯示圖像查看效果：

%matplotlib inline
import cv2
from matplotlib import pyplot as plt
import numpy as np

def show(img, code=cv2.COLOR_BGR2RGB):
    cv_rgb = cv2.cvtColor(img, code)
    fig, ax = plt.subplots(figsize=(16, 10))
    ax.imshow(cv_rgb)
    fig.show()

img = cv2.imread('1.jpg')
show(img)

OpenCV 中默認是 BGR 通道，通過 cvtColor 函數將原圖轉換成灰度圖：

img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

邊緣檢測

有了灰度圖之後，接下來用 Canny 邊緣檢測算法檢測邊緣。

Canny 邊緣檢測算法主要是以下幾個步驟：

• 用高斯濾波器平滑圖像去除噪聲干擾（低通濾波器消除高頻噪聲）。

• 生成每個點的亮度梯度圖（intensity gradients），以及亮度梯度的方向。

• 通過非極大值抑制（non-maximum suppression）縮小邊緣寬度。非極大值抑制的意思是，只保留梯度方向上的極大值，刪除其他非極大值，從而實現銳化的效果。

• 通過雙阈值法（double threshold）尋找潛在邊緣。大於高阈值為強邊緣（strong edge），保留；小於低阈值則刪除；不大不小的為弱邊緣（weak edge），待定。

• 通過遲滯現象（Hysteresis）處理待定邊緣。弱邊緣有可能是邊緣，也可能是噪音，判斷標准是：如果一個弱邊緣點附近的八個相鄰點中，存在一個強邊緣，則此弱邊緣為強邊緣，否則排除。

在 OpenCV 中可以直接使用 Canny 函數，不過在那之前要先用 GaussianBlur 函數進行高斯模糊：

img_gb = cv2.GaussianBlur(img_gray, (5, 5), 0)

接下來使用 Canny 函數檢測邊緣，選擇 100 和 200 作為高低阈值：

edges = cv2.Canny(img_gray, 100 , 200)

執行結果如下：

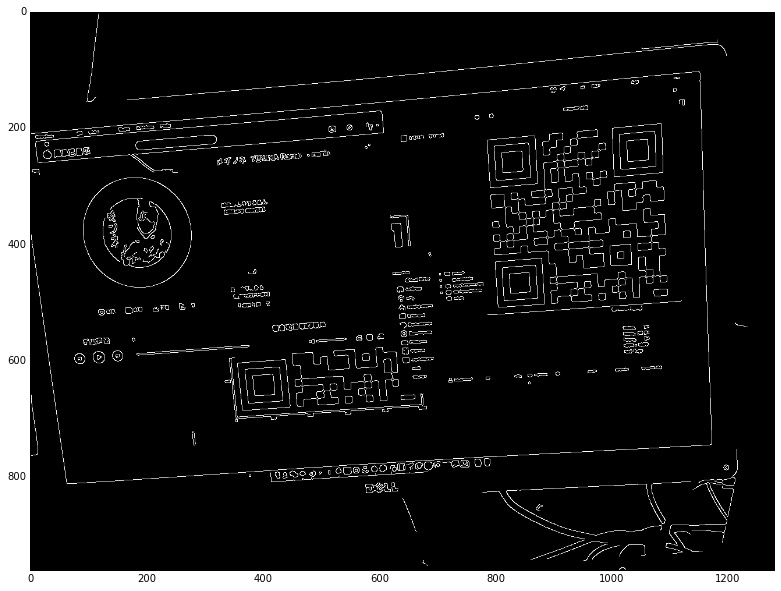
可以看到圖像中的很多噪音都被處理掉了，只剩下了邊緣部分。

尋找定位標記

有了邊緣之後，接下來就是通過輪廓定位圖像中的二維碼。二維碼的 Position Detection Pattern 在尋找輪廓之後，應該是有6層（因為一條邊緣會被識別出兩個輪廓，外輪廓和內輪廓）：

所以，如果簡單處理的話，只要遍歷圖像的層級關系，然後嵌套層數大於等於5的取出來就可以了：

img_fc, contours, hierarchy = cv2.findContours(edges, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

hierarchy = hierarchy[0]
found = []
for i in range(len(contours)):
    k = i
    c = 0
    while hierarchy[k][2] != -1:
        k = hierarchy[k][2]
        c = c + 1
    if c >= 5:
        found.append(i)

for i in found:
    img_dc = img.copy()
    cv2.drawContours(img_dc, contours, i, (0, 255, 0), 3)
    show(img_dc)

繪制結果如下：

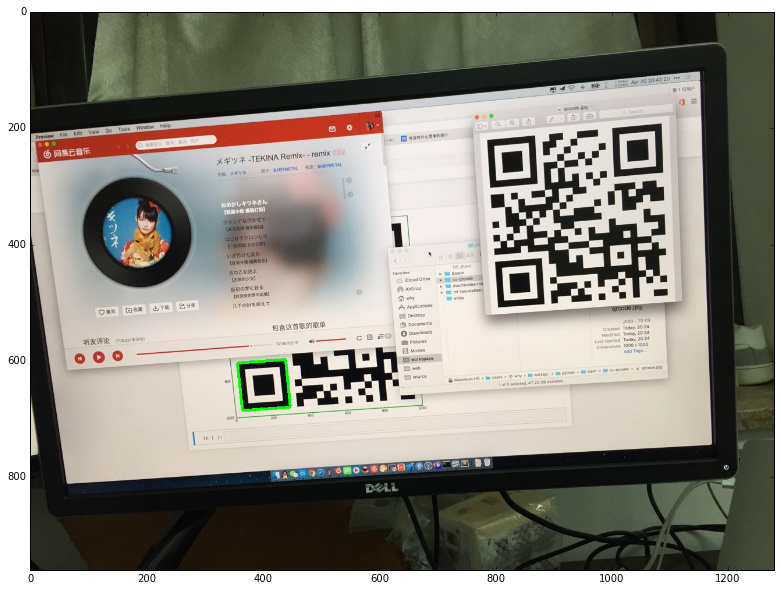
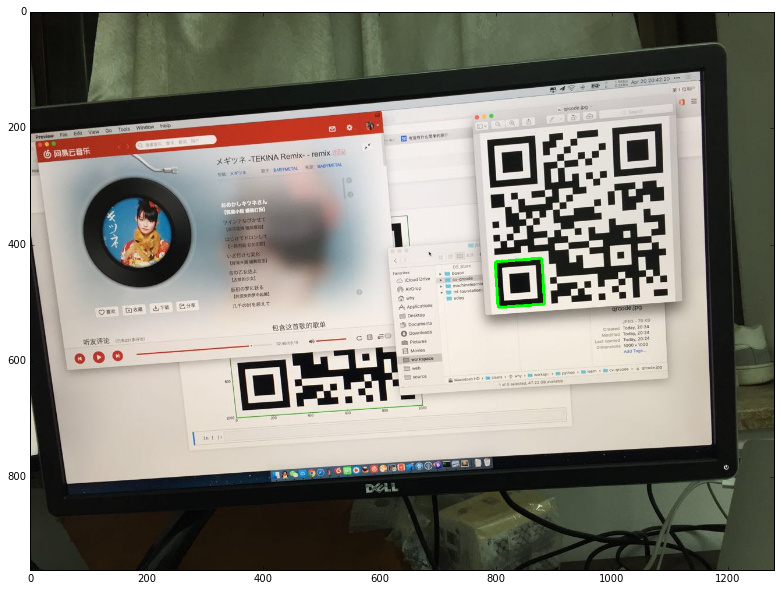
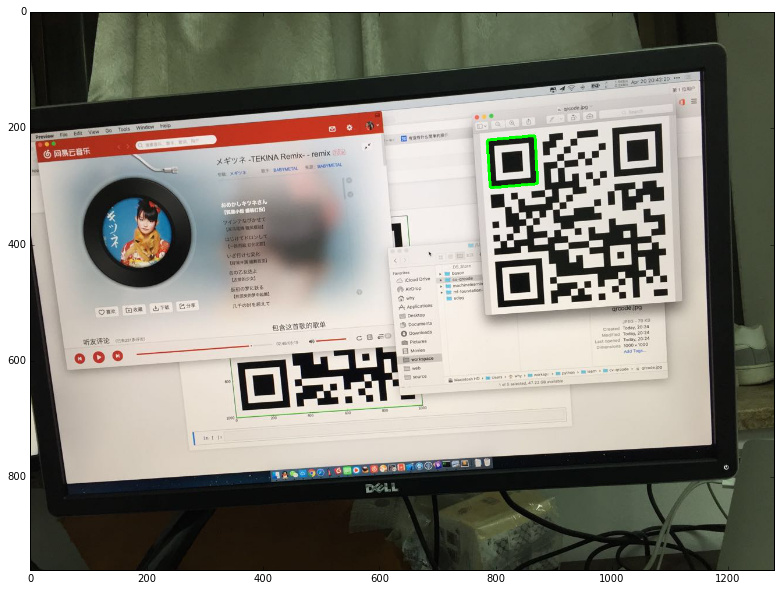
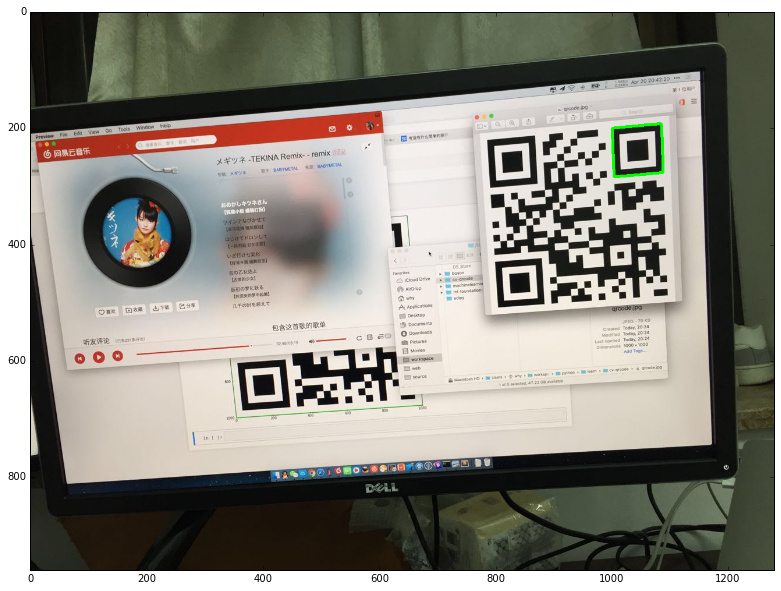
定位篩選

接下來就是把所有找到的定位標記進行篩選。如果剛好找到三個那就可以直接跳過這一步了。然而，因為這張圖比較特殊，找出了四個定位標記，所以需要排除一個錯誤答案。

講真，如果只靠三個 Position Detection Pattern 組成的直角三角形，是沒辦法從這四個當中排除錯誤答案的。因為，一方面會有形變的影響，比如斜躺著的二維碼，本身三個頂點連線就不是直角三角形；另一方面，極端情況下，多余的那個標記如果位置比較湊巧的話，完全和正確結果一模一樣，比如下面這種情況：

所以我們需要 Timing Pattern 的幫助，也就是定位標記之間的黑白相間的那兩條黑白相間的線。解決思路大致如下：

• 將4個定位標記兩兩配對

• 將他們的4個頂點兩兩連線，選出最短的那兩根

• 如果兩根線都不符合 Timing Pattern 的特征，則出局

尋找定位標記的頂點

找的的定位標記是一個輪廓結果，由許多像素點組成。如果想找到定位標記的頂點，則需要找到定位標記的矩形包圍盒。先通過 minAreaRect 函數將檢查到的輪廓轉換成最小矩形包圍盒，並且繪制出來：

draw_img = img.copy()
for i in found:
    rect = cv2.minAreaRect(contours[i])
    box = cv2.boxPoints(rect)
    box = np.int0(box)
    cv2.drawContours(draw_img,[box], 0, (0,0,255), 2)
show(draw_img)

繪制如下：

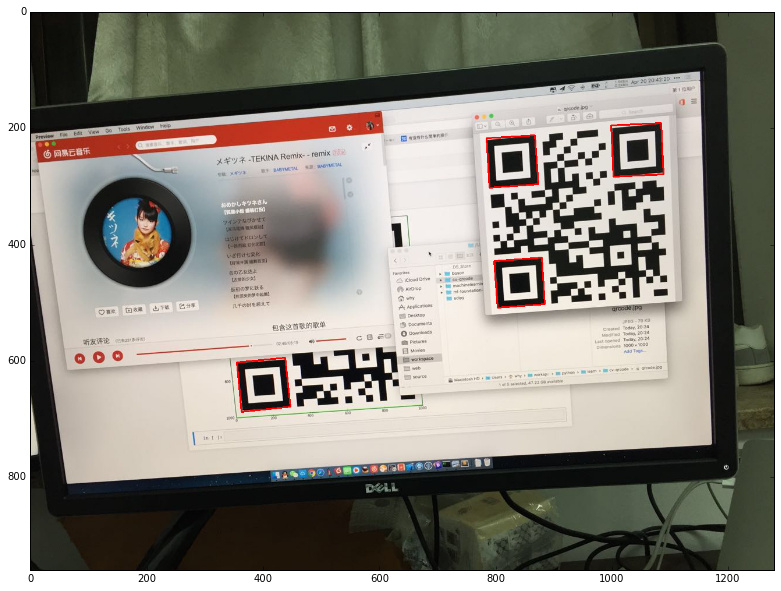
這個矩形包圍盒的四個坐標點就是頂點，將它存儲在 boxes 中：

boxes = []
for i in found:
    rect = cv2.minAreaRect(contours[i])
    box = cv2.boxPoints(rect)
    box = np.int0(box)
    box = map(tuple, box)
    boxes.append(box)

定位標記的頂點連線

接下來先遍歷所有頂點連線，然後從中選擇最短的兩根，並將它們繪制出來：

def cv_distance(P, Q):
    return int(math.sqrt(pow((P[0] - Q[0]), 2) + pow((P[1] - Q[1]),2)))

def check(a, b):
    # 存儲 ab 數組裡最短的兩點的組合
    s1_ab = ()
    s2_ab = ()
    # 存儲 ab 數組裡最短的兩點的距離，用於比較
    s1 = np.iinfo('i').max
    s2 = s1
    for ai in a:
        for bi in b:
            d = cv_distance(ai, bi)
            if d < s2:
                if d < s1:
                    s1_ab, s2_ab = (ai, bi), s1_ab
                    s1, s2 = d, s1
                else:
                    s2_ab = (ai, bi)
                    s2 = d              
    a1, a2 = s1_ab[0], s2_ab[0]
    b1, b2 = s1_ab[1], s2_ab[1]
    # 將最短的兩個線畫出來
    cv2.line(draw_img, a1, b1, (0,0,255), 3)
    cv2.line(draw_img, a2, b2, (0,0,255), 3)

for i in range(len(boxes)):
    for j in range(i+1, len(boxes)):
        check(boxes[i], boxes[j])
show(draw_img)

繪制結果如下：

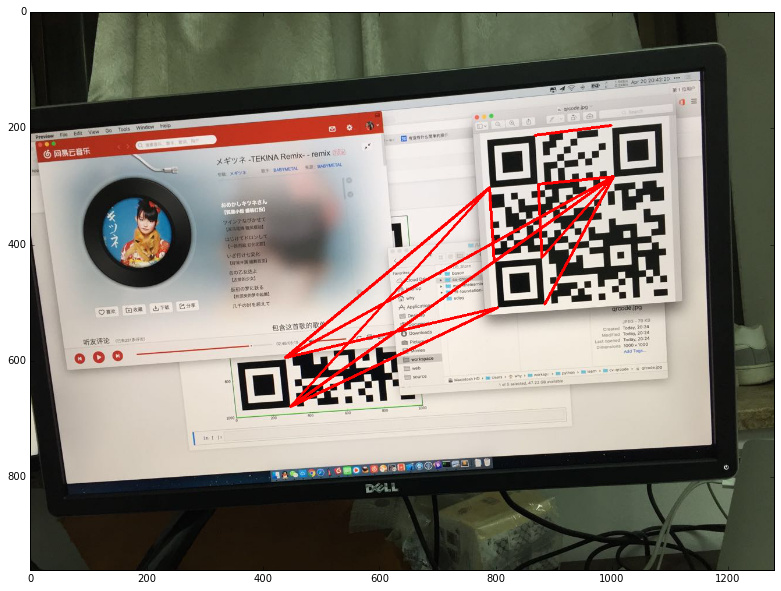
獲取連線上的像素值

有了端點連線，接下來需要獲取連線上的像素值，以便後面判斷是否是 Timing Pattern 。

在這之前，為了更方便的判斷黑白相間的情況，先對圖像進行二值化：

th, bi_img = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY)

接下來是獲取連線像素值。由於 OpenCV3 的 Python 庫中沒有 LineIterator ，只好自己寫一個。在《OpenCV 3.0 Python LineIterator》這個問答裡找到了可用的直線遍歷函數，可以直接使用。

以一條 Timing Pattern 為例：

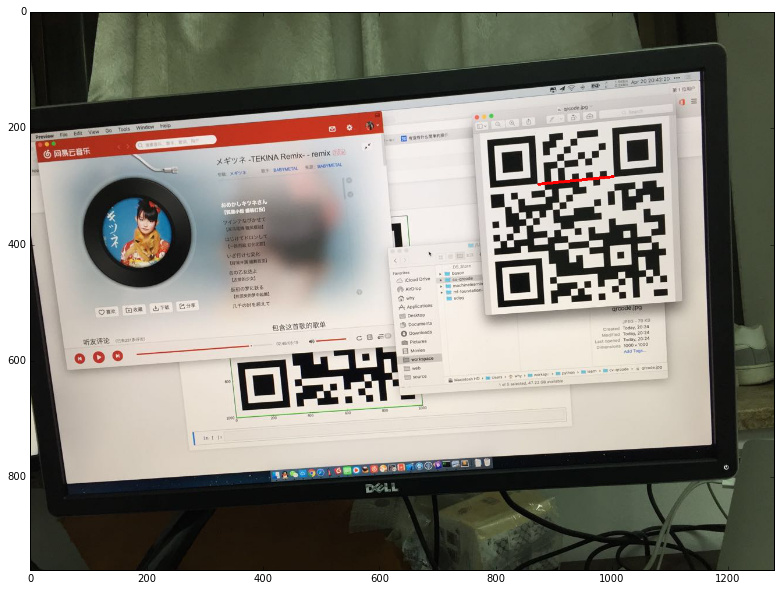
打印其像素點看下結果：

[ 255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.  255.  255.  255.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
    0.    0.    0.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.    0.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.]

修正端點位置

照理說， Timing Pattern 的連線，像素值應該是黑白均勻相間才對，為什麼是上面的這種一連一大片的結果呢？

仔細看下截圖可以發現，由於取的是定位標記的外部包圍盒的頂點，所以因為誤差會超出定位標記的范圍，導致沒能正確定位到 Timing Pattern ，而是相鄰的 Data 部分的像素點。

為了修正這部分誤差，我們可以對端點坐標進行調整。因為 Position Detection Pattern 的大小是固定的，是一個 1-1-3-1-1 的黑白黑白黑相間的正方形，識別 Timing Pattern 的最佳端點應該是最靠裡的黑色區域的中心位置，也就是圖中的綠色虛線部分：

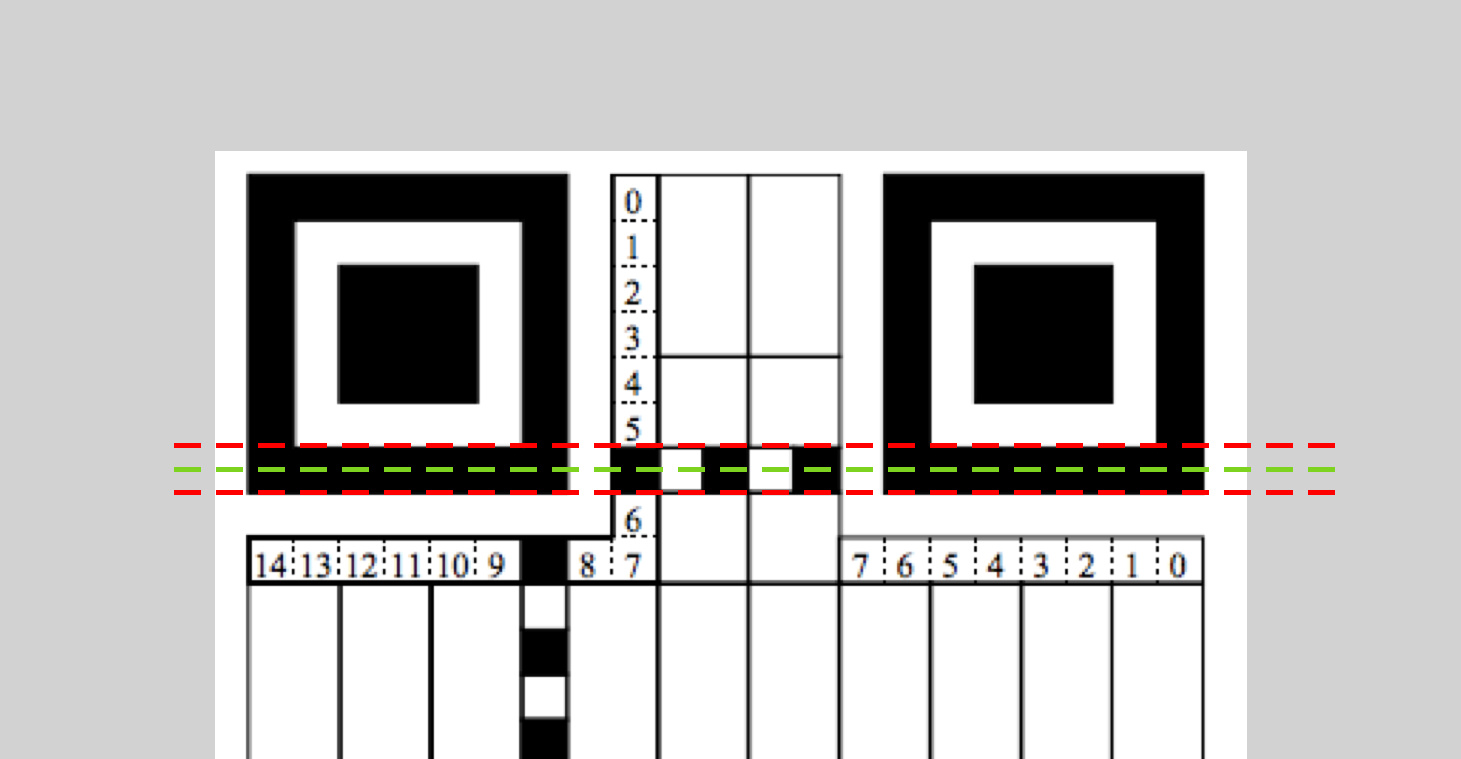
所以我們需要對端點坐標進行調整。調整方式是，將一個端點的 x 和 y 值向另一個端點的 x 和 y 值靠近 1/14 個單位距離，代碼如下：

a1 = (a1[0] + (a2[0]-a1[0])*1/14, a1[1] + (a2[1]-a1[1])*1/14)
b1 = (b1[0] + (b2[0]-b1[0])*1/14, b1[1] + (b2[1]-b1[1])*1/14)
a2 = (a2[0] + (a1[0]-a2[0])*1/14, a2[1] + (a1[1]-a2[1])*1/14)
b2 = (b2[0] + (b1[0]-b2[0])*1/14, b2[1] + (b1[1]-b2[1])*1/14)

調整之後的像素值就是正確的 Timing Pattern 了：

[ 255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.]

驗證是否是 Timing Pattern

像素序列拿到了，接下來就是判斷它是否是 Timing Pattern 了。 Timing Pattern 的特征是黑白均勻相間，所以每段同色區域的計數結果應該相同，而且旋轉拉伸平移都不會影響這個特征。

於是，驗證方案是：

• 先除去數組中開頭和結尾處連續的白色像素點。

• 對數組中的元素進行計數，相鄰的元素如果值相同則合並到計數結果中。比如 [0,1,1,1,0,0] 的計數結果就是 [1,3,2] 。

• 計數數組的長度如果小於 5 ，則不是 Timing Pattern 。

• 計算計數數組的方差，看看分布是否離散，如果方差大於阈值，則不是 Timing Pattern 。

代碼如下：

def isTimingPattern(line):
    # 除去開頭結尾的白色像素點
    while line[0] != 0:
        line = line[1:]
    while line[-1] != 0:
        line = line[:-1]
    # 計數連續的黑白像素點
    c = []
    count = 1
    l = line[0]
    for p in line[1:]:
        if p == l:
            count = count + 1
        else:
            c.append(count)
            count = 1
        l = p
    c.append(count)
    # 如果黑白間隔太少，直接排除
    if len(c) < 5:
        return False
    # 計算方差，根據離散程度判斷是否是 Timing Pattern
    threshold = 5
    return np.var(c) < threshold

對前面的那條連線檢測一下，計數數組為：

[11, 12, 11, 12, 11, 12, 11, 13, 11]

方差為 0.47 。其他非 Timing Pattern 的連線方差均大於 10 。

找出錯誤的定位標記

接下來就是利用前面的結果除去錯誤的定位標記了，只要兩個定位標記的端點連線中能找到 Timing Pattern ，則這兩個定位標記有效，把它們存進 set 裡：

valid = set()
for i in range(len(boxes)):
    for j in range(i+1, len(boxes)):
        if check(boxes[i], boxes[j]):
            valid.add(i)
            valid.add(j)
print valid

結果是：

set([1, 2, 3])

好了，它們中出了一個叛徒，0、1、2、3 四個定位標記，0是無效的，1、2、3 才是需要識別的 QRCode 的定位標記。

找出二維碼

有了定位標記之後，找出二維碼就輕而易舉了。只要找出三個定位標記輪廓的最小矩形包圍盒，那就是二維碼的位置了：

contour_all = np.array([])
while len(valid) > 0:
    c = found[valid.pop()]
    for sublist in c:
        for p in sublist:
            contour_all.append(p)

rect = cv2.minAreaRect(contour_ALL)
box = cv2.boxPoints(rect)
box = np.array(box)

draw_img = img.copy()
cv2.polylines(draw_img, np.int32([box]), True, (0, 0, 255), 10)
show(draw_img)

繪制結果如下：

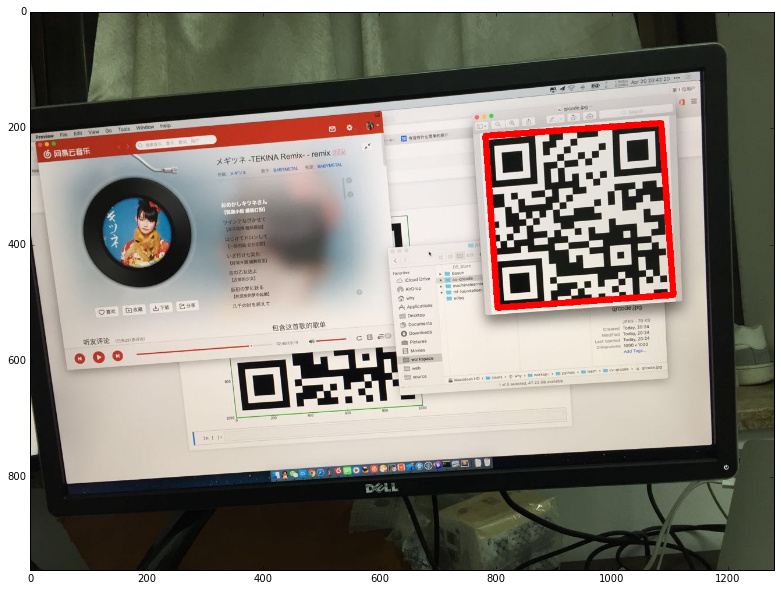
小結

後面仿射變換後坐標修正的問題實在是寫不動了，這篇就先到這裡吧。

回頭看看，是不是感覺繞了個大圈子？

『費了半天勁，只是為了告訴我第0個定位標記是無效的，我看圖也看出來了啊！』

是的，不過代碼裡能看到的只是像素值和它們的坐標，為了排除這個錯誤答案確實花了不少功夫。

不過這也是我喜歡做數字圖像處理的原因之一：可用函數數不勝數，專業概念層出不窮，同樣的一個問題，不同的人去解決，就有著不同的答案，交流的過程便是學習的過程。

啊對了，如果有更好的解決方案，歡迎在評論裡指出！

以及，文章裡有一個紅包彩蛋，你找到了嗎 =。=

財富！名譽！地位！窮得叮當響的海賊汪，哥爾·D·汪海，他在臨睡前的一句話讓人們趨之若鹜奔向博客：『想要我的紅包嗎？想要的話可以全部給你，去找吧！我把所有紅包都放在那裡！』

參考文獻：

• 二維碼的生成細節和原理

• What is a QR code?

• ISO/IEC 18004: QRCode Standard

• What Are The Different Sections In A QR Code?

• Decoding small QR codes by hand

• How data matrix codes work

• QR Code Tutorial

• How to Read QR Symbols Without Your Mobile Telephone

• OpenCV: QRCode detection and extraction

• Tutorial Python: Contours Hierarchy

• Wiki: Pixel Connectivity

• Image Processing: Connect

• Wiki: Image Moment

• Wiki: Moment (Mathematics))

• 圖像的矩特征

• 統計數據的形態特征

• 圖像的矩（Image Moments）

• OpenCV Doc: Structural analysis and shape descriptors

• CS7960 AdvImProc MomentInvariants

• OpenCV Doc: Canny

• Wiki: Canny Edge Detector

• Wiki: Hysteresis

• OpenCV 3.0 Python LineIterator