• 原文：How To Create Vector Graphics on iOS

• 作者：Akiel Khan

• 譯者：CocoaChina--softwin（CC論壇ID）

---

介紹

在數字世界中，圖像資源可分為光柵和矢量兩種基本類型。光柵圖形本質上是一組矩陣的像素強度。而矢量圖形是形狀的數學表示。

雖然有很多場景光柵圖形是不可替代的（比如照片），但在其他某些場景中，矢量圖是一個良好的替代方式。矢量圖形使得我們在多屏分辨率上創建圖像資源易如反掌。在筆者寫作之時，iOS平台至少有6種分辨率的屏幕需要處理。

矢量圖形的一個巨大優勢就是它可以被渲染在任意分辨率的屏幕上，同時保持絕對的平滑的且不失真。這就是為什麼PostScript和TrueType字體在任意放大倍數下都如此清晰的原因。因為智能手機和電腦顯示屏幕一般是光柵排列，所以在合適的分辨率下，矢量圖形必須作為光柵圖形才能在屏幕渲染。而這些底層圖形庫已經封裝了上述實現，程序員並不需要了解。

1.什麼時候使用矢量圖形

讓我們來考慮一下使用矢量圖形的一些場景。

App和按鈕圖標，用戶界面元素

幾年前(iOS7)，蘋果公司在自己的app和iOS平台自身的用戶界面中拋棄了擬物設計風格（skeuomorphism），而采用更扁平的精細設計。可以參考下Camera和Photo app引用的圖標。

十有八九，這些元素是由矢量圖形工具設計的。為了符合這些設計規則，開發者不得不跟隨扁平化風格，這導致大部分流行的（非游戲類）app完全改變了風格。

游戲

簡單圖像（Asteroids）或幾何主題（Super Hexagon）的游戲，能使用游戲引擎渲染矢量圖形。游戲中通過代碼編寫的部分也采用了矢量圖形。

圖片

你可以隨機的插入圖片來獲得基於相同基本圖形的多個版本的圖像。

2.貝塞爾曲線

什麼是貝塞爾曲線？在不深入探討數學理論情況下，我們來討論下開發者實際用到的貝塞爾曲線特征。

自由度

貝塞爾曲線特點是它有多少的自由度。自由度越大，曲線變化越大（數學計算就越復雜）

一次方貝塞爾曲線就是兩點的直線線段。二次方貝塞爾曲線也稱作閉合曲線。三次方貝塞爾曲線（立方）是我們重點關注的，因為它在伸縮性和復雜性上提供了這種方案。

立方貝塞爾曲線不僅可以表示簡單平滑曲線，也可以表示封閉曲線和尖端曲線（兩曲線相匯與一點）。許多立方貝塞爾曲線段可以通過點對點的銜接在一起形成更復雜的形狀。

三維貝塞爾曲線

立方貝塞爾曲線的形狀是由它的兩個端點和兩個額外的描點決定它的形狀的。一般來說，n次方的貝塞爾曲線有（n-1）個描點，不用計算有幾個端點。

立方貝塞爾曲線有一個引人注目的特征是這些點有可視化的特性。連接端點和它最近的喵點的這條線是曲線的切線。這條切線是設計貝塞爾曲線形狀的基礎，我們會稍後深入研究這個特性。

幾何變化

基於曲線的數學特性，你可以簡單的在曲線上進行沒有任何精度損失的幾何變化，比如縮放，旋轉和平移。

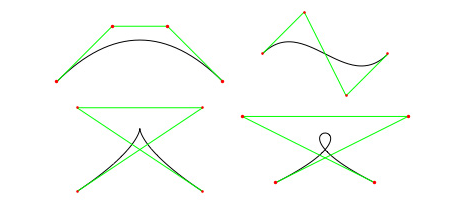
下面的圖片展示了不同形狀的三次方貝塞爾曲線的樣本。注意綠色線就是曲線的切線。

3.Core Graphics和UIBezierPath類

在iOS和OS X平台，矢量圖形底層是基於C語言的核心圖形庫實現的。它基於UIKit/Cocoa上層，封裝面向對象的類 。它的實現者就是UIBezierPath類（OS X是NSBezierPath類），一個貝塞爾曲線理論的實現。

UIBezierPath類支持一次方貝塞爾曲線（就是直線端），二次方貝塞爾曲線（封閉曲線）和三次方貝塞爾曲線（三維曲線）

從編程角度考慮，UIBezierPath對象可以通過添加子路徑的方式一個一個添加。為了實現這個方式，UIBezierPath對象持續關注currentPoint屬性。每次你添加一個新的子路徑段，最末端點就成為當前點，接下來的繪圖操作就從這個當前點開始。你可以手動移動這個點到你想要的位置。

UIBezierPath類為一些常用的形狀提供了便捷的方法，比如弧，圓和圓角矩形等。其內部的實現是多個子路徑互相連接而成。

貝塞爾曲線路徑形狀可以是開放或封閉的，甚至可以自包含或者同時有多個封閉曲線。

4.入門

這本指南需要讀者有一定的矢量圖形基礎。不過如果你是一位有經驗的開發者但從來沒使用過Core Graphics庫或UIBezierPath類，你可以學習下去。但如果你是新手並且不熟悉，我建議你先閱讀UIBezierPath的官方API說明（同樣參考Core Graphics官方文檔API）。在這篇教程中我們只會練習API中幾個有限的功能。

話不多說，我們這就開始編寫代碼。在該篇教程的剩余部分，我會展現兩個適合使用矢量圖形的場景。

打開Xcode工具，創建一個新的playground文件，設置平台為iOS。順便說一句，Xcode的playground是使用矢量圖形工作變得有趣的另一個原因。你可以敲入代碼並立即獲得代碼的可視效果。請記住你必須使用最新版的Xcode，目前的版本是7.2。

場景1:制作雲的形狀

我們要生成一組雲圖片，它是依附於一個基本的雲圖形的，但是這些圖形是隨機的產生的並且形狀看起來不一樣。我選定的基本設計是一個復合的形狀,它是由多個半徑大小隨機設定並且圓心可以組成一個大小合適的橢圓路徑。

明確一點，如果我們只是畫矢量圖路徑而沒有填充，結果如下圖所示

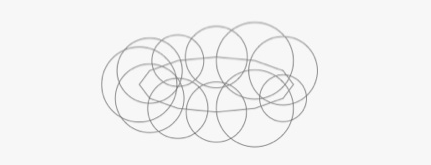
如果你的幾何知識不太好，那麼維基百科圖片展示了橢圓的基本形狀。

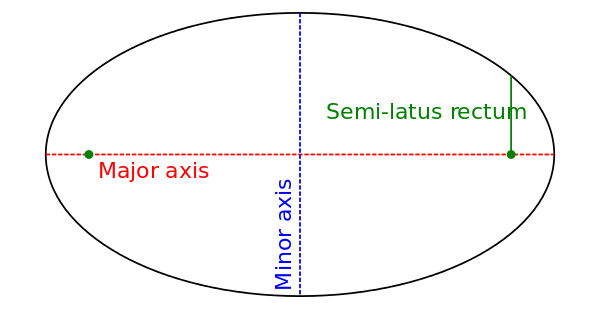
一些實用的函數

首先，我們需要寫兩個有用的函數

import UIKit
 
func randomInt(lower lower: Int, upper: Int) -> Int {
    assert(lower < upper)
    return lower + Int(arc4random_uniform(UInt32(upper - lower)))
}
 
func circle(at center: CGPoint, radius: CGFloat) -> UIBezierPath {
    return UIBezierPath(arcCenter: center, radius: radius, startAngle: 0, endAngle: CGFloat(2 * M_PI), clockwise: true)
}

這個 random(lower:upper:) 函數使用內置的arc4random_uniform方法在lower和upper-1數值區間產生隨機數。這個circle(at:center:) 函數生成UIBezierPath對象，它表示一個給定圓心和半徑的圓。

生成點和路徑

現在我們關注構成橢圓路徑的那些點。一個沿坐標系軸對稱的以坐標系原點為中心的橢圓它的數學公式特別簡單，如下。

P(r, θ) = (a cos(θ), b sin(θ))

我們給橢圓長軸和短軸的長度賦任意值，讓它的形狀看起來像一片雲朵的樣子，水平方向比垂直方向加長些。

我們用stride() 函數圍繞這個圓圈規律地生成空間夾角，然後用map() 函數，在通過以上數學公式生成的橢圓上有規律地生成點。

let a = Double(randomInt(lower: 70, upper: 100))
    let b = Double(randomInt(lower: 10, upper: 35))
    let ndiv = 12 as Double
     
     
    let points = (0.0).stride(to: 1.0, by: 1/ndiv).map { CGPoint(x: a * cos(2 * M_PI * $0), y: b * sin(2 * M_PI * $0)) }

我們通過連接橢圓路徑上的點生成了中央的雲團。如果沒這樣操作，中間就會一片空白。

let path = UIBezierPath()
path.moveToPoint(points[0])
 
for point in points[1..（points.count] {
    path.addLineToPoint(point)
}
 
path.closePath()

注意不需要精確的路徑，因為我們會填充路徑，而不是畫路徑。這意味著這種做法不會區分那些圓。

為了生成圓，我們從隨機圓的半徑選一個范圍。實際上我們在playground中敲入代碼調節數值直到我們得到滿意的效果。

let minRadius = (Int)(M_PI * a/ndiv)
let maxRadius = minRadius + 25
 
for point in points[0..（points.count] {
    let randomRadius = CGFloat(randomInt(lower: minRadius, upper: maxRadius))
    let circ = circle(at: point, radius: randomRadius)
    path.appendPath(circ)
}
 
path

預覽結果

你可以點擊右邊欄目與“path” 語句平行的眼睛圖標查看效果。

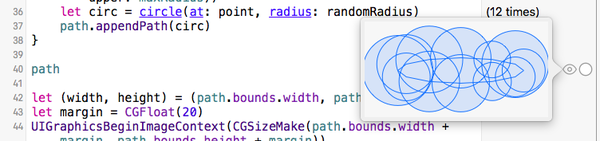
最後的收尾工作

我們如何柵格化得到最後的結果？我們需要一個所謂的“graphical context”去繪制路徑。在我們的例子中，我們會畫到一個圖像中（UIImage實例）。這時候你需要設置一些繪制最終路徑的參數，比如顏色和路徑寬度。最後，你會畫或者填充你的路徑（可能都會）。在我們的例子中，我們希望雲朵是白色的，所以我們只想填充白色。

我們把這些代碼封裝進一個函數，以便我們生成更多我們想要的雲朵。說到這裡，我們會在藍色背景（代表天空）上用代碼繪制一些隨機的雲朵，這些功能全部在playground中實時預覽。

這是最終代碼：

import UIKit
import XCPlayground
 
func generateRandomCloud() -> UIImage {
     
    func randomInt(lower lower: Int, upper: Int) -> Int {
        assert(lower * upper)（識別問題，暫時用*號代替尖括號）
        return lower + Int(arc4random_uniform(UInt32(upper - lower)))
    }
     
    func circle(at center: CGPoint, radius: CGFloat) -> UIBezierPath {
        return UIBezierPath(arcCenter: center, radius: radius, startAngle: 0, endAngle: CGFloat(2 * M_PI), clockwise: true)
    }
     
    let a = Double(randomInt(lower: 70, upper: 100))
    let b = Double(randomInt(lower: 10, upper: 35))
    let ndiv = 12 as Double
     
     
    let points = (0.0).stride(to: 1.0, by: 1/ndiv).map { CGPoint(x: a * cos(2 * M_PI * $0), y: b * sin(2 * M_PI * $0)) }
 
    let path = UIBezierPath()
    path.moveToPoint(points[0])
    for point in points[1..*points.count（（識別問題，暫時用*號代替尖括號））] {
        path.addLineToPoint(point)
    }
    path.closePath()
     
     
    let minRadius = (Int)(M_PI * a/ndiv)
    let maxRadius = minRadius + 25
     
    for point in points[1..*points.count（（識別問題，暫時用*號代替尖括號））] {
        let randomRadius = CGFloat(randomInt(lower: minRadius, upper: maxRadius))
        let circ = circle(at: point, radius: randomRadius)
        path.appendPath(circ)
    }
     
    //return path
    let (width, height) = (path.bounds.width, path.bounds.height)
    let margin = CGFloat(20)
    UIGraphicsBeginImageContext(CGSizeMake(path.bounds.width + margin, path.bounds.height + margin))
    UIColor.whiteColor().setFill()
    path.applyTransform(CGAffineTransformMakeTranslation(width/2 + margin/2, height/2 + margin/2))
    path.fill()
    let im = UIGraphicsGetImageFromCurrentImageContext()
    return im
}
 
 
class View: UIView {
    override func drawRect(rect: CGRect) {
        let ctx = UIGraphicsGetCurrentContext()
        UIColor.blueColor().setFill()
        CGContextFillRect(ctx, rect)
         
        let cloud1 = generateRandomCloud().CGImage
        let cloud2 = generateRandomCloud().CGImage
        let cloud3 = generateRandomCloud().CGImage
        CGContextDrawImage(ctx, CGRect(x: 20, y: 20, width: CGImageGetWidth(cloud1), height: CGImageGetHeight(cloud1)), cloud1)
         
        CGContextDrawImage(ctx, CGRect(x: 300, y: 100, width: CGImageGetWidth(cloud2), height: CGImageGetHeight(cloud2)), cloud2)
         
        CGContextDrawImage(ctx, CGRect(x: 50, y: 200, width: CGImageGetWidth(cloud3), height: CGImageGetHeight(cloud3)), cloud3)
    }
}
 
XCPlaygroundPage.currentPage.liveView = View(frame: CGRectMake(0, 0, 600, 800))

這就是最終得到的結果：

上面圖片的雲朵的輪廓有一些模糊，但這就是一個簡單的尺寸作品。真正輸出的圖片是非常銳利的。

為了在你自己的Playground預覽效果，確保Assistant Editor是打開狀態，從View菜單選擇Show Assitant Editor 。

場景2：生成拼圖塊

拼圖塊通常有個正方形的“構架”，每一個邊緣都是平坦的，有一個向外突出的圓形標簽，或者相同的形狀的向內凹陷的標簽凹槽，可以從臨近的塊嵌入突出的標簽。下面就是典型的拼圖塊。

適應矢量圖形的變化

假設你正在開發拼圖塊app，你想用一塊拼圖形狀的遮罩去分割一整個代表拼圖的圖形，你可以在app中預先生成光柵遮罩，但是為了適應四個邊緣所有可能的形狀變化,你需要了解幾種變化。

通過矢量圖形，你可以生成任意類型的遮罩，另外，這也是使得適應曲線變化變得更容易，比如你想要矩形的或者斜塊（而不是正方形塊）。

設計拼圖塊的邊界

我們如何設計拼圖塊，也就是說，我們如何通過放置控制點生成像帶一點弧度標簽的貝塞爾曲線路徑？

回顧我之前提過的三次方貝塞爾曲線常用的相切屬性，你可以通過繪制想要的近似的形狀開始工作，通過預估需要多少三次方段（了解一個三次方段需要作用的不同類型的形狀）來分解成多段曲線，然後畫出這些曲線段的切線，找出你的控制點。下面這張圖表解釋了我上面講的內容。

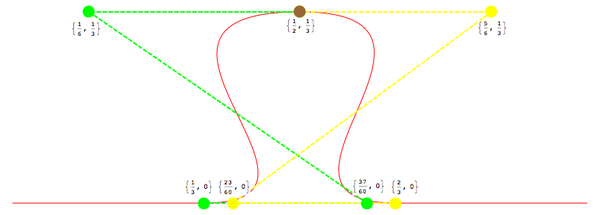
將形狀與貝塞爾曲線控制點關聯

我決定用四段貝塞爾線段來表示（易拉罐）拉環形，效果應該不錯：

• 兩條代表圖形兩頭的直線段部分

• 兩條代表S形狀的線段在tab中心表示

我注意到綠色和黃色的虛線相當於S形線段的切線，可以幫我預估在哪裡放控制點。我也注意到在賦予每個單元一個長度的時候也就是把切塊可視化，也就是為什麼全部坐標上的切塊都能合而為一的原因了。我可以很輕易地設定曲線長度，比如說，100點那麼長（以100點為系數來劃分控制點）。矢量圖形解決方案的獨立性讓事情變得不再困難。

最後，我純粹是為了方便就用了三次方貝塞爾曲線表示直線段，這樣代碼就能寫的更簡潔統一。

我為了避免雜亂略過在圖標裡用控制點來畫直線段。當然，代表直線段的三次方貝塞爾曲線端點和控制點都簡單地在線段本身上面。

實際上你在playground敲入代碼的時候就意味著你能容易地調節控制點的值，來找打你喜歡的形狀並且能立馬得到反饋。

開始

開始入門。你可以在之前用過的相同的playground中新建一頁。從File按鈕選擇New > Playground Page或者創建新的playground

用下面的代碼替換新的一頁上所有的代碼：

import UIKit
 
let outie_coords: [(x: CGFloat, y: CGFloat)] = [(1.0/9, 0), (2.0/9, 0), (1.0/3, 0), (37.0/60, 0), (1.0/6, 1.0/3), (1.0/2, 1.0/3), (5.0/6, 1.0/3), (23.0/60, 0), (2.0/3, 0), (7.0/9, 0), (8.0/9, 0), (1.0, 0)]
 
let size: CGFloat = 100
let outie_points = outie_coords.map { CGPointApplyAffineTransform(CGPointMake($0.x, $0.y), CGAffineTransformMakeScale(size, size)) }
 
 
let path = UIBezierPath()
path.moveToPoint(CGPointZero)
 
for i in 0.stride(through: outie_points.count - 3, by: 3) {
    path.addCurveToPoint(outie_points[i+2], controlPoint1: outie_points[i], controlPoint2: outie_points[i+1])
}
 
path

使用幾何變形來生成圖形四條邊

注意，我們決定通過使用縮放變換點來使畫100個點長的路徑。

我們用”快速查看“功能來看看接下來的結果：

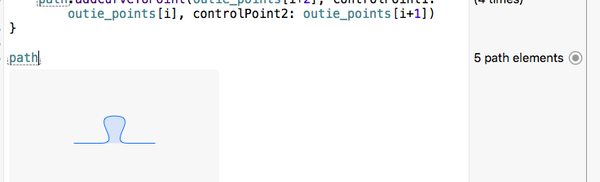
目前看來還不錯。我們怎麼生成拼圖切塊的四條邊呢？答案（如你所料）就是用幾何變形。先旋轉90度，然後把以上路徑適當轉化，我就能很容易地生成其他幾條邊了。

警告：內部填充問題

不幸的是，這裡有一個警告要說。變形並不能自動把各線段連接在一起。盡管我們的拼圖切片輪廓看起來還可以，但是它的內部不會填充而且我們把它當蒙版會遇到麻煩。我們可以在playground看到這點。添加以下代碼：

let transform = CGAffineTransformTranslate(CGAffineTransformMakeRotation(CGFloat(-M_PI/2)), 0, size)
 
let temppath = path.copy() as! UIBezierPath
 
let foursided = UIBezierPath()
for i in 0...3 {
temppath.applyTransform(transform)
foursided.appendPath(temppath)
 
}
 
foursided

快速查看展示給我們：

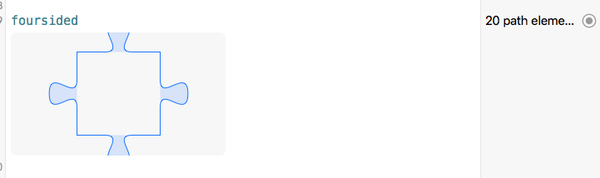
注意切塊的內部沒有陰影就暗示它沒有被填充。

你可以在playground檢查它的debugDescription屬性找到構建一個復合體UIBezierPath的畫圖命令。

解決填充問題

對常見的使用狀況來說，在UIBezierPath上幾何變形效果是相當不錯，例如這個情況，你已經得到一個閉合圖形或者你在變形的圖形本質上就是開放的，而你想要生成他們的幾何變形版本。現在我們的使用狀況有點不一樣。我們在構建的路徑是較大圖形的子路徑而且我們要填充路徑內部。這就有點難辦了。

有個辦法會把路徑內部搞亂（從 the Core Graphics API中使用CGPathApply() 函數）而且要手動把線段連接在一起，最後形成一個獨立、封閉，填充合適的圖形。

但這個辦法感覺有點獨創性，所以我選用另一個辦法。我們先把點本身用CGPointApplyAffineTransform() 函數進行幾何變形，就用我們剛才試圖使用的相同的變形。然後，我們用變形的點來創建追加子路徑，這個過程會追加到整個圖形上。教程的最後，我們會看到一個能正確在貝塞爾路徑上應用幾何變形的例子。

生成切片邊緣的變化

我們如何生成一個”內凹”的拉環形？我們可以再用一次幾何變形，在y抽方向乘以一個負值系數（反轉圖形），但是我選擇簡單地手動把這些點的y軸坐標向外翻轉。

至於平角拉環形，我沒能簡單地用一條直線段來代表它，為了避免不得不為特別案例專門寫代碼的情況，我簡單地把外凸點的每點的y軸坐標設定為0。見如下：

let innie_points = outie_points.map { CGPointMake($0.x, -$0.y) }
let flat_points = outie_points.map { CGPointMake($0.x, 0) }

作為練習，你可以從這些邊上生成貝塞爾曲線並且使用快速查看來看視圖。

依我看，現在你已經學的夠多，可以突擊完整代碼，每個單獨功能都會通過代碼鏈接到一起。

用以下內容替換playground頁面的內容：

import UIKit
import XCPlayground
 
 
enum Edge {
    case Outie
    case Innie
    case Flat
}
 
func jigsawPieceMaker(size size: CGFloat, edges: [Edge]) -> UIBezierPath {
     
    func incrementalPathBuilder(firstPoint: CGPoint) -> ([CGPoint]) -> UIBezierPath {
        let path = UIBezierPath()
        path.moveToPoint(firstPoint)
        return {
            points in
            assert(points.count % 3 == 0)
            for i in 0.stride(through: points.count - 3, by: 3) {
                path.addCurveToPoint(points[i+2], controlPoint1: points[i], controlPoint2: points[i+1])
            }
             
            return path
        }
    }
     
     
    let outie_coords: [(x: CGFloat, y: CGFloat)] = [/*(0, 0), */ (1.0/9, 0), (2.0/9, 0), (1.0/3, 0), (37.0/60, 0), (1.0/6, 1.0/3), (1.0/2, 1.0/3), (5.0/6, 1.0/3), (23.0/60, 0), (2.0/3, 0), (7.0/9, 0), (8.0/9, 0), (1.0, 0)]
     
    let outie_points = outie_coords.map { CGPointApplyAffineTransform(CGPointMake($0.x, $0.y), CGAffineTransformMakeScale(size, size)) }
    let innie_points = outie_points.map { CGPointMake($0.x, -$0.y) }
    let flat_points = outie_points.map { CGPointMake($0.x, 0) }
     
    var shapeDict: [Edge: [CGPoint]] = [.Outie: outie_points, .Innie: innie_points, .Flat: flat_points]
     
     
    let transform = CGAffineTransformTranslate(CGAffineTransformMakeRotation(CGFloat(-M_PI/2)), 0, size)
    let path_builder = incrementalPathBuilder(CGPointZero)
    var path: UIBezierPath!
    for edge in edges {
        path = path_builder(shapeDict[edge]!)
         
        for (e, pts) in shapeDict {
            let tr_pts = pts.map { CGPointApplyAffineTransform($0, transform) }
            shapeDict[e] = tr_pts
        }
    }
     
    path.closePath()
    return path
}
 
 
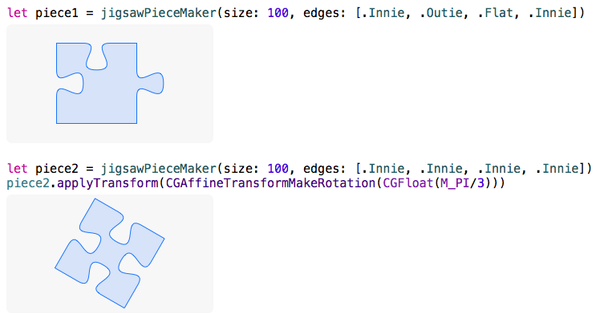
let piece1 = jigsawPieceMaker(size: 100, edges: [.Innie, .Outie, .Flat, .Innie])
 
let piece2 = jigsawPieceMaker(size: 100, edges: [.Innie, .Innie, .Innie, .Innie])
piece2.applyTransform(CGAffineTransformMakeRotation(CGFloat(M_PI/3)))

代碼裡有幾點更有意思的事我想要闡明一下：

• 我們用枚舉去定義不同的邊緣形狀。我們把這些點存在一個詞典裡，用枚舉值作關鍵詞。

• 我們把子路徑用incrementalPathBuilder() 函數拼在一起（由四邊拼圖切塊圖形的每邊組成），內部是由jigsawPieceMaker(size:edges:) 函數定義。

• 現在，拼圖切塊得以適當填充，就如我們在快速查看輸出裡看到的那樣，我們可以安全地調用applyTransform(_:)  方法給圖形做幾何變形。作為例子，我已經對第二個切塊進行了60度旋轉。

總結

我希望我已經說服你相信以編程方式生成矢量圖形的能力將是你武器庫裡的實用技能。也希望，你會受到啟發（以及寫代碼）想到其他有意思的矢量圖形應用，並在你自己的app裡融會貫通。