前提：端點的數為1.
1、每個數等於它上方兩數之和。
2、每行數字左右對稱，由1開始逐漸變大。
3、第n行的數字有n項。
4、第n行數字和為2^(n-1)。
5、第n行的第m個數和第n-m+1個數相等，即C(n-1,m-1)=C(n-1,n-m)，這是組合數性質
性質6的公式表述
之一
6、每個數字等於上一行的左右兩個數字之和。可用此性質寫出整個楊輝三角。即第n+1行的第i個數等於第n行的第i-1個數和第i個數之和，這也是組合數的性質之一。（公式見右圖）

 

 

int n;

scanf("%d",&n);
int i,j,k,a[n][n];//i控制行，j控制列
for(i=0;i<n;i++){

a[i][0]=1;a[i][i]=1;//行的第一個和最後一個為1

}

for(i=2;i<n;i++){
for(j=1;j<=i-1;j++){

a[i][j]=a[i-1][j]+a[i-1][j-1];//等於正上方和它前一個的和

}
}

//下面打印等腰的楊輝三角

for(i=0;i<n;i++){
//k控制空格

for(k=0;k<n-1-i;k++){
printf("      ");
}

for(j=0;j<=i;j++){
printf("%6d      ",a[i][j]);
}

printf("/n");

}

 

 

 

 

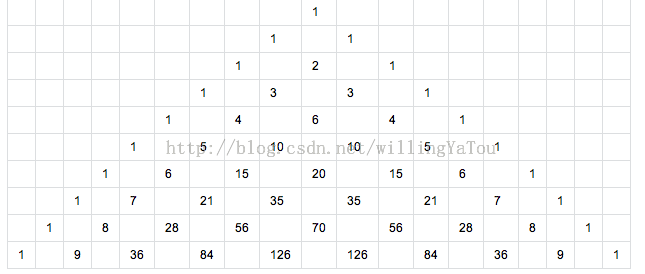
輸入：10

打印：

 

 

 

－－－